Оглавление:

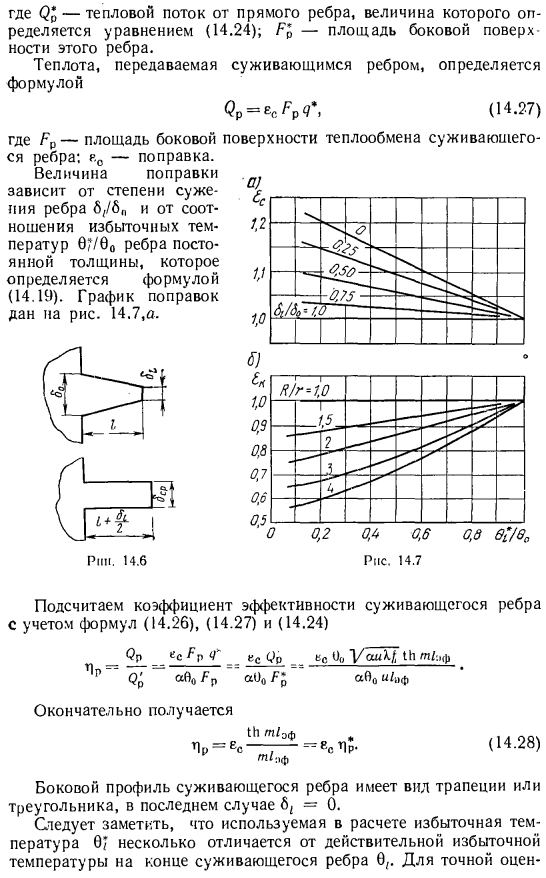


Коэффициент эффективности ребер с изменяющимся поперечным сечением
- В прямых и кольцевых (цилиндрических) конических ребрах, а также в кольцевых ребрах определенной толщины площадь поперечного сечения ребер, через которые проходит тепловой поток, и периметр этого сечения изменяются по длине ребер. Поэтому, принимая во внимание тепловой баланс реберных элементов, это приведет к таким случаям Уравнения потенциала, интегрируемые в цилиндрические функции (функции Бесселя), и формулы для оценки температурных полей и тепловых потоков даже на длинных кромках имеют довольно сложный вид.
Для газов формулу (8-17) можно несколько упростить, так как в этом случае величина критерия Прандтля близка к единице, а поэтому знаменатель 270 можно считать постоянным. Людмила Фирмаль
Учитывая несоответствие расчетной схемы и реальных условий теплопередачи с помощью коррекции, рассмотрим простой метод расчета ребер, поперечное сечение которых изменяется по длине ребер, основанный на замене ребер прямыми ребрами определенной толщины. Упрощенный метод обеспечивает ту же точность, что и расчет по формуле, полученной прямым интегрированием дифференциальных уравнений. На рисунке 14.6 показано прямое коническое ребро и его конструктивная схема. Прямая кромка определенной толщины, принятая в качестве расчетной схемы, имеет ту же ширину, что и расчетная кромка, а ее длина и толщина определяются уравнением.
- Плотность теплового потока от поверхности ребер определенного сечения равна. Где(22-тепловой поток от прямой кромки, а его величина определяется по формуле (14.24). P-площадь боковой поверхности этого ребра. Тепло, передаваемое коническими ребрами, определяется по формуле СР = р: м *>(ч-27) Где Rp-площадь теплопередающей стороны конического ребра. Рассчитайте коэффициент полезного действия конических ребер с учетом формул (14.26), (14.27) и (14.24 Наконец-то узнал (14.28)) Поперечный профиль сужающегося ребра представляет собой трапециевидную или треугольную рейку, в последнем случае 6 = 0.
Обратите внимание, что избыточная температура, используемая в расчете, равна 6.Незначительно отличается от фактической избыточной температуры края конических ребер. Для точной оценки Необходимо использовать формулу, полученную путем интегрирования дифференциального уравнения температурного поля и величины₍0 и конической кромки. Аналогично, теплопередача рассчитывается для кольцевых ребер определенной толщины. Схема такого ребра (рис. 14.8) представляет собой прямое ребро шириной 1 м, толщина которого равна толщине кольцевого ребра, а длина равна И= ’ Чт. (1⁴-2⁹) Где/?А г-внешние и Рисунок 14.8 Писать внутренний радиус реберной кости.
В рассматриваемом случае отношение длины трубки к ее диаметру равно 100, поэтому большая часть потока являет- ся гидравлически стабилизированной и, следовательно, расчеты можно производить по формуле (8-13). Людмила Фирмаль
Тепловой поток через кольцевое ребро и его коэффициент полезного действия определяются по следующей формуле: (?грабли ^ п?*>(14-30) Чр = 8 и ’ — ^ ^ — = EKL;. (14.31) поправочный коэффициент е определяется с использованием рисунка. Коэффициент 14.7, B избыточная температура 0, * / 0°и радиусное отношение/?/ Г Кольцевое ребро почти возможно В случае истощения (14.32) (14.33) Где плотность теплового потока. Рассчитывается на плоских ребрах шириной 1 м, длина рассчитывается по формуле (14.29), толщина равна половине толщины кольцевых ребер у основания и на концах. Поправки rn и rf определяются из рисунка.
Смотрите также:
| Теплопередача через ребристую стенку | Излучающие ребра |
| Температурное поле и коэффициент эффективности прямых ребер постоянной толщины | Ребристая стенка минимальной массы |

