Свободная энергия и максимальная работа.

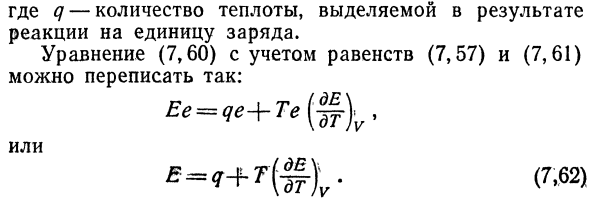
Свободная энергия и максимальная работа.

• Свободная энергия и максимальная производительность. Уравнение Гиббса Гельмгольца Необратимые изотермические свойства Формат технологического соотношения G, 44) имеет вид: Даллас, г, 49） Увеличение свободной энергии В этом случае в системе выполняется меньше работы. Если формула G, 45′) интегрирована Начальное и конечное состояние системы、

Тогда можно определить работу W = Fi-F2. Необратимый процесс Вт> Ф2-ФВ Это следует  Получается, что при заданном состоянии оно обратимо Процесс между этими условиями. Макс. Максимальная работа равна разнице в свободной энергии. Эти 2 Государства： Ш Ф-Ф Макс — * 1l2 * 11 В. Ф.

Самая большая работа, которую может сделать система Совершить при изотермическом процессе между 2 Людмила Фирмаль

Ноздрев 161 найти уравнение максимальной работы. Для этого Используйте уравнение Гиббса Гельмгольца. Легко получить из объединения формул G, 9) и G, 12) Формат такой: Предположим, что система переходит изотермически Из одного состояния в другое. Затем%первый и государства м ： Л-С + Р ^. GD）） И во 2-м государстве： (^). Г, 50 ’）

Найдите разницу в свободной энергии в 2-х состояниях. Равный максимальному процесс работы： Ш ^ ^ ф — ф ^ У. — У. + т ^ ф — ф ^ г, г, 51） Или ВДМ = — А(/ + Т(^ П») К, Г, 52） Куда? С самого начала процесса равенства Форма термодинамики (B, 9) является: Или Гв ^ У2-Уи = dU1 г, 53）

• Тогда, если вы присваиваете значение dU равенству G, то 51）、 。 Г, 54） Уравнение G, 54) называется максимальным уравнением* Ноя work. It устанавливает взаимосвязь между теплотой и Эффект и максимальная реакция во время определенной работы* Т и в *

Электродвижущая сила гальванического Элементы Посмотрите на соотношение гальванической ЭДС. Элементы, характеризующие другие параметры

Как пример использования свободы* Энергия для решения термодинамической задачи Людмила Фирмаль

Состояние системы. Рассмотреть дело В случае обратимого изотермического процесса. Писать Выражение работы гальванического элемента： d’w = Ede, G, 55） Где E-электродвижущая сила элемента, e-электрический заряд、 Он протекает через цепь во время изотермического процесса. Принимая во внимание уравнение G, 45), получим: ДФ = — Эде> г, 56） Или Форекс-Ф2 = УО, Г, 57）

То есть работа, выполняемая гальваническими элементами、 Равна разности между 1-й и 2-й свободной энергией Состояние it. To найдите эту разницу、 Уравнение Гиббса-Гельмгольца для обоих состояний： Г, 58） Г, 59） \ В  / г Отсюда ФЛ-Р2 ^ = Ул-У2 — \ — ТВт (ФЛ-Ф2) В. Г, 60） Мы покажем Ул-У2 = = qе, г, 61） Где q-количество тепла, выделяющегося в результате Реакция на единицу заряда. Уравнение G, 60)уравнение G, 57) и G, 61)

Вы можете переписать его следующим образом. Разница выражает количество E и Q через Ф4-Ф2、 из равенства q1-u2a G, 57)- FF G, 63） Е И из равенства G, 61） д.- ^=^= Г, 64） Из Формулы G, 62), G, 63), G, 64) мы видим: ДТ) г-С-он =} [(Ля.^- ( ^ — ^)]. Г, 65） И я думаю, что F = U-TS、 Мы получаем： Или Где S2-5i-разность между конечной и начальной энтропией Состояние гальванической батареи. T = Const для интегрирования выражения d ’ Q = TdS、

Присвоить результат равенству G, 66) и, наконец, Мы получаем： 2Л \ — ВОПРОС WJv-e• Где Q-количество тепла, которое получает элемент Термостат. е. д. с гальванической Если гальванический элемент увеличивается, т. е.-> 0, то количество Электричество работает потому что тепло положительное Химическая энергия элемента

Приток тепла от термостата. — dtr-для <0, Q <0.In этот случай, часть химиката Химическая энергия элемента выделяется в виде тепла、 Подойдите к термостату. Сто шестьдесят четыре Поэтому, используя термодинамику Связь между параметрами способа, гальваническая Пустой элемент. Потому что очень много химических реакций Изотермически свободная энергия используется особенно часто Используется в химической термодинамике.

Смотрите также:

Решение задач по термодинамике

Соотношение взаимности.	Свободная энергия равновесных систем.
Физический смысл понятия свободной энергии.	Тепловая функция. Эффект Джоуля Томсона.