Оглавление:




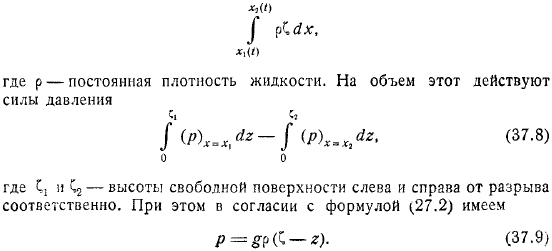

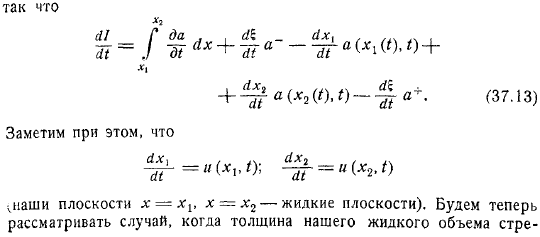



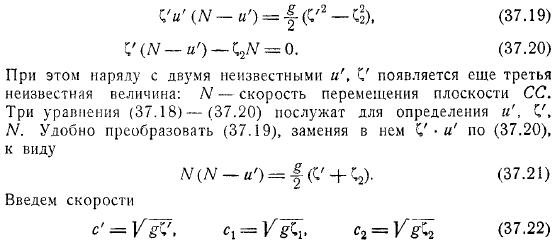



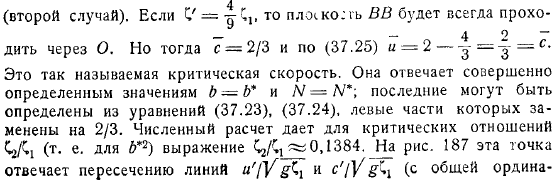

Длинные волны конечной амплитуды. Волны на мелкой воде. Разрушение плотины
При выводе основных уравнений гидромеханики длинных волн мы сделали предположения: предположение о возможности игнорирования вертикального ускорения, предположение о возможности игнорирования вертикальной силы помимо силы тяжести и предположение о малой амплитуде колебаний жидкости. В этом разделе мы снимаем 3-е предположение и рассматриваем длинные волны конечной амплитуды. Примерами проблем, связанных здесь, являются разрушение плотин, разрушение волн, обтекание берега, препятствия в случае мелководных водоемов.
В этих задачах предположение о малой амплитуде становится неточным, а остальные предположения теории длинных волн оправдываются. Для плоского движения несжимаемой жидкости приведем явное уравнение. Но теперь это не так.
- Замените и напишите вместо этого. Когда мы выводили уравнение из уравнения, мы игнорировали нелинейные члены.
- Здесь центры действия атмосферы поэтому мы этого делать не будем, а возьмем основное уравнение длинной волны вида.
Для пространственных движений, если есть скорости, по аналогии (дно горизонтальное) и уравнение согласуется с уравнением плоской нестационарной задачи о движении сжимаемого тела. Людмила Фирмаль
Имеет особую форму зависимости давления от плотности. Политропный процесс с политропными индикаторами.
Движение сжимаемых жидкостей подробно описано в части этого курса, глава газовая динамика. Метод, описанный в главе газовая динамика, может быть перенесен на рассмотрение соответствующей задачи о длинных волнах на поверхности воды. В настоящее время мы не обсуждаем общие решения.
- Однако он ограничивается рассмотрением характерного примера применения уравнения. В качестве примера рассмотрим проблему разрушения плотины.
- В первый раз вертикальная перегородка длинны волны Бора укладывается с левой и правой сторон, прилегающих к ней, соответственно, сохраняя неподвижный слой воды толщиной в равновесии.
Пусть это будет конкретика. Раздел будет удален внезапно. Вам нужно найти ходы. Рассматриваемое дифференциальное уравнение является уравнением. Из этого необходимо определить функции (соответственно, скорость и высоту свободной поверхности).
Наше движение, начавшееся с разрыва нужной функции, продолжает сопровождаться разрывом. Людмила Фирмаль
Прежде всего, необходимо вывести условия в промежутке. Это условие должно удовлетворять искомой функции (на ходу).
Чтобы вывести эти условия, обратимся к закону сохранения импульса и массы. Предположим, у вас есть движение, которое происходит, когда есть промежуток. Рассмотрим вертикальную поверхность, состоящую из частиц жидкости на левой стороне поверхности разрушения.
Пусть действуют законы ее движения. Рассмотрим также плоскость справа от прерывистой поверхности. Пусть она знает законы движения. Рассмотрим закон движения поверхности зазора. Рассмотрим массу воды, заключенную между двумя вертикальными плоскостями, которые движутся вместе с водой.
Импульс этой текучей массы. Постоянная плотность жидкости. На этот объем влияет. В этом случае высота свободной поверхности будет находиться соответственно слева и справа от зазора. Также по формуле. Сделайте приращение импульса равным импульсу силы.
Где находится разрыв функции в интервале интегрирования в точке? Если он приближается к этой плоскости, то если он остается на левой стороне, он указывает на значение, полученное в плоскости. Если вы приближаетесь к плоскости справа, укажите полученное значение.
Это различие называется разрыв и показано следующим образом. Вы можете написать как это. Мы отмечаем, что сейчас. Подумайте о случае, когда толщина нашего объема жидкости представляет собой поток. Стремится к нулю, но разрыв остается внутри (из-за этого), тогда интеграл справа стремится к нулю и.
Это будет очевидно. Итак, мы получаем условия на момент прыжка. Внешний (результат). Это скорость разрыва. Вернемся к проблеме разрушения плотин. Рассмотрим различных области в воде. Прежде всего, это водоемы (левый и правый края).
Есть постельный режим, а уровень имеет. Начальные значения (в поле) и (в поле). Площадь совпадает с площадью вдоль. В этой области жидкость движется, и это движение непрерывно сопряжено с остальной областью.
Позиция плоская. Скорость и движение в пределах региона можно определить в любое время. Кроме того, площадь совпадает с площадью в плоскости. Скорость и уровень поверхности непрерывно перемещаются от значений в области к значениям в области снова.
После этого (в регионе) они остаются постоянными. Эти последние величины сопряжены с остальной площадью вдоль поверхности, где они также претерпевают скачок. Далее покажем, как найти скорость движения поверхности и скорость прерывистой поверхности, а также движение жидкости в этой области.
В этой области существует самоподобное решение системы (оно мешает началу оси в точке, где в первый момент располагалась плотина). Я ищу решение следующего формата. Тогда мы получим систему уравнений где.
Решение для этой системы получается в следующем виде где произвольная константа. Этот метод должен быть, если область совокупляется, есть скорость движения плоскости. Во соотношении найти размер скорости, потому что она должна быть из ниоткуда.
Это скорость распространения волны на поверхности. Поэтому движение в пределах площади плоскости определяется. Эта область характеризуется постоянной постоянной скоростью и постоянным уровнем.
Эти неизвестные величины должны быть связаны следующим соотношением. Кроме того, сопряжение движения в области происходит вдоль прерывистого. Принимает в. Необходимо записать условия для присоединения движений.
В то же время, наряду с неизвестными, отображается неизвестная величина, скорость самолета. Формулы помогут вам. Сердце, удобно преобразованное и замененное в нем. Я собираюсь показать вам скорость.
И безразмерное количество. Не только отношение. Из уравнения вы легко получите следующее уравнение. Безразмерное уравнение принимает вид. Таким образом, мы можем знать (то есть определить отношение из уравнения. Отображается значение функции отношения начальной высоты воды.
Отметим, что подъем воды во время движения после разрушения плотины имеет максимальное значение (вблизи точки этот максимум составляет примерно от начальной высоты воды на левой стороне плотины). В крайнем случае движения воды по сухому руслу мы получим. Этот результат получается непосредственно из анализа формулы.
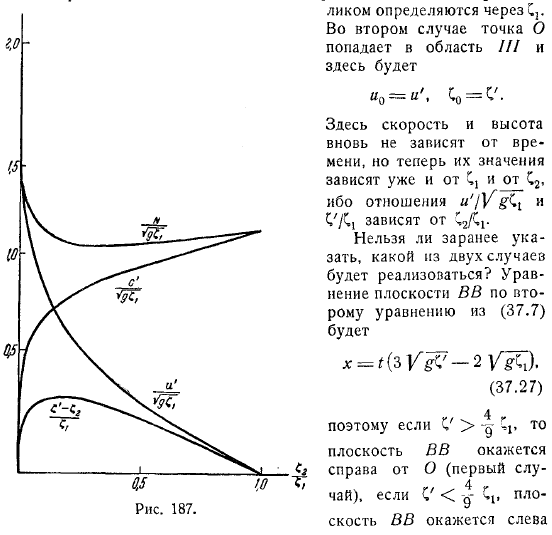
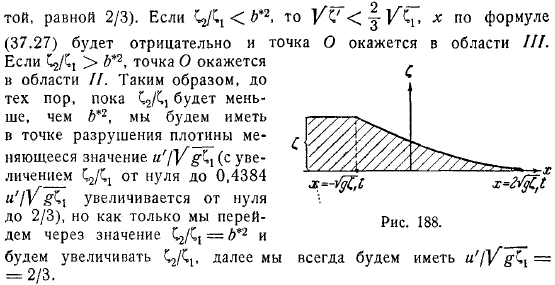
Дело схематично нарисовано. Интересно, что функцией времени является изучение движения того места, где изначально находилась плотина. Есть случая. Это тот случай, когда плоскость рисуется с правой стороны от начального положения плотины и на.
В первом случае точка находится в регионе, и движение в этой точке происходит полностью. Это зависит только от формулы, которую вы. Другими словами, скорость и высота не зависят от времени и высоты лицо решительное.
Во случае точка падает на площадь. Опять же, скорость и высота не зависят от времени, но их значения уже зависят. Зависит от отношений. Можно ли заранее указать, какое из дел будет реализовано?
Уравнение плоскости по уравнению из (отсюда, если самолет находится слева, то самолет будет справа (в первом случае (случай). Если его самолет всегда будет проходить. Это так называемая критическая скорость.
Это соответствует четко определенному значению, последнее можно определить из уравнения, и его левая часть заменяется. Численные расчеты дают уравнение критического отношения. Эта точка соответствует пересечению линий (в обычном порядке равно).
По выражению точка будет отрицательной, если она отображается в области. Поэтому величина будет меняться в точке разрушения плотины до тех пор, пока она не станет меньше ее от нуля он увеличивается (от нуля), но как только он превышает значение, он продолжает увеличиваться. У нас всегда есть.

