Закон Вина.

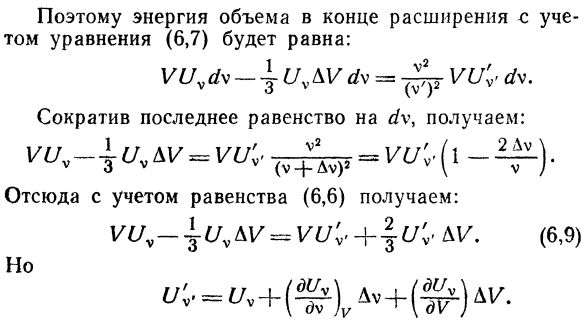
Закон Вина.

• Рассмотрим адиабатическое расширение Шар, наполненный черным излучением Полностью отражающая стена. Если шар расширяется Равномерно и бесконечно медленно, после этого твердеть будет испытан Вы испытаете обратимый адиабатический процесс. Стена шара движется、 Отраженные от них световые волны меняются、

Кроме того, модифицированная длина волны Ф 5） Где А /?Является ли увеличение радиуса шара с течением времени A / Уровень инфляции бал Формулу F, 5) можно переписать в виде: Я-3 з ф Или — 3В ’ Где V-объем шара, а V-частота излучения.: ВН / = const и Ф 60 Укажите частоты предварительного и последующего расширения соответственно* 

Когда вы интегрируете это уравнение, вы получаете: Людмила Фирмаль

На самом деле, в v и v’, объемы V и V, и они выглядят так: Или （ Откуда (v’k y ’+ 3(v7J dv ’ Vr * = v3 ^ + 3v2 dv V. Из последнего уравнения это выглядит так: V’(v’jdv’ ^ Vv2dv. Ф 7.） Создайте объем с полностью отражающей стеной Заполняется черным излучением температуры Т Укажите энергию и частоту единицы измерения дозы облучения в Увдв между V и V + ДВ、

Определяет Увс. Лучистая энергия объема V равна VUvdv. Увеличение увеличение объема при дв сопровождается работой излучения. Кроме того, радиационное давление стенок р = л (Jvdv. Ф 8） Работа с этим процессом термоизоляции Излучение, вызванное уменьшением внутренней энергии Energy. At конец расширения, внутренняя энергия В у з ДВ = ДВ вуф-п дв、 Или В у з * ДВ = ДВ вуф—птенец ДВ ООО/.

• Таким образом, энергия объема в конце расширения равна Рассматривая уравнение F, 7) выглядит так: ВР ДВ. Если вы уменьшите последнее равенство до d\, это выглядит так: Отныне, рассматривая уравнение F, 6) получаем. Вуф-jUvAV ^ вю тоже.- }- юрвав. 9) заменить последнее равенство Av на равенство F, 6), получаем следующее： Замените полученное выражение уравнением 9) дайте： Последнее уравнение удовлетворяется решением Да.： {/Ф, 10）

Где F-неопределенная функция. В процессе изоляции. Отношение F, 2). С D’q = 0, замените E из представления закона Стефана — Больцман F, 4）： Или e =0Г4, так что、 ^ L__3il поводья Если мы интегрируем это равенство、 \ nV = — в 3G + const、 Откуда V7 * = const, F, 12） Перепишите формулу F и 10) учтите последнюю Соотношение： (Ф) взлетел）

Соотношение между температурой и объемом. Людмила Фирмаль

Это выражение является законом смеха* Ниябина. Некоторые термодинамические методы без дополнительных Допущения не позволяют определить вид функции f. Когда мы переходим от изучения частоты к исследованию Exdk—установка длины волны в том месте, где заряжается энергия единичного объема Излучение длин волн на границе между A и X + dX、 И с тех пор есть v-F-dv-P

Венский закон можно переписать в следующем виде: 5 F, 14） Экспериментальная зависимость E%от фиксированного A Фиксированная температура построенная для различных температур Температура, если Amax-длина волны、 Соответствует максимальному значению A、 K * KST = const F, 15） Разверните форму функции f в Формуле Венского закона

Возможна формула излучения планка.Закон Стефана Больцмана Этот закон был впервые экспериментировал с Однако она была установлена Стефаном и впоследствии подтверждена в теории Больцман ждал. Излучение можно считать нормальным Термодинамическая система.

Внутренняя энергия такова Система U = eV9 F, 1） Где e (T) — плотность энергии, а V-объем системы. Дифференциал энтропии такой системы принимает вид: ТДВ + ^ дв Ф 2） Энтропия s (ТВ)

Состояния и dS все производные, со следующим V, мы найдем： д(В ДГ \ дд \ д предполагая, что r (T) зависит только от температуры、 Мы получаем уравнение.： Узнай, на что решиться! е ’ * oG4, Ф 4） Где а = 7.64-10〜15 erg / deg * — cm Ishi 1.82-10〜22 кал / Град 4 X Икс? Л * 3.Выражение F, 4) и представляют закон Стефан Больцман, плотность соответственно Энергия излучения пропорциональна 4 градусам Температура.

Смотрите также:

Решение задач по термодинамике

Закон Кирхгофа.	Формула излучения Планка.
Давление излучения.	Термодинамические функции.