Оглавление:




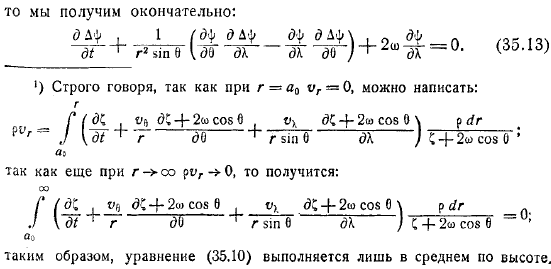


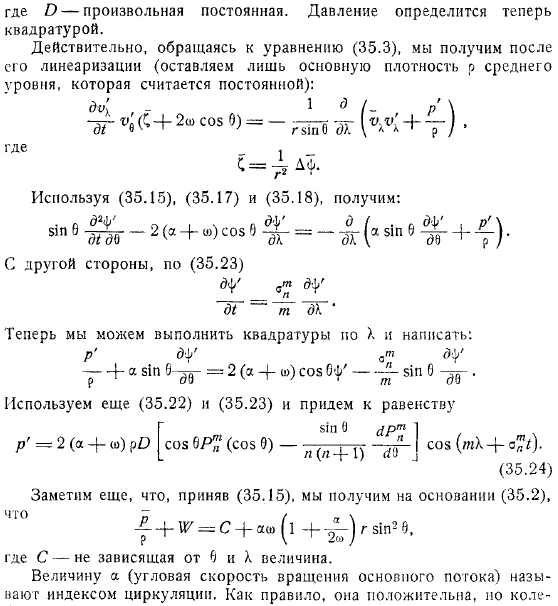


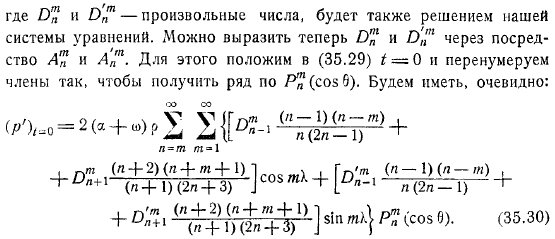

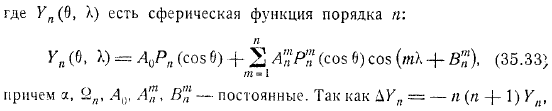


Волны во вращающейся атмосферной оболочке
Рассмотрим неподвижные длинные волны, которые формируются в атмосфере Земли. Последний захватывается вращением. Кроме того, в общих чертах земная атмосфера всегда. Начинается на определенной высоте и происходит движение Востока и Запада (атмосфера как бы обгоняет землю своим восточным и западным вращением).
Получить сферическую систему координат, связанную с вращением. Показано умножением широты на расстояние от центра Земли и долготы от одного Меридиана до другого. Компонент скорости вдоль меридиана (положительный, если скорость направлена на юг) и компонент скорости внутри круга широт (положительный, если скорость направлена на Восток).
- Напишите уравнение движения в виде барана. Здесь, как и прежде, рассматриваются возможности гравитации, включая силу притяжения Ньютонов и центробежную силу вращения Земли, а последний раздел справа представляет силу Кориолиса.
- Опишите компоненты этого уравнения вдоль оси и, согласно длинноволновому методу, проигнорируйте следующие термины.
Компонент скорости вдоль оси. Людмила Фирмаль
Уравнение неразрывности. В связи с этим движение атмосферы может быть значительно упрощено. То есть гидромеханика в таком движении, в отличие от задач нелинейной акустики и газовой динамики, с течением времени изменение плотности при движении в горизонтальном направлении мало по сравнению с плотностью.
Кроме того, толщина (порядок) активной части атмосферы невелика по сравнению с радиусом Земли, так что вместо нее можно писать очень точно. Умножаем с обеих сторон, дифференцируя полученное выражение, а затем вычитаем производную. Получить в счет сделайте Землю сферой радиуса.
- Тогда нам нужно. Кроме того, если необходимо учитывать (атмосфера не теряется и не приобретает массу извне). Но тогда есть такая высота, чтобы достичь максимума).
- Где же он? Предположим теорию приливов , что существует по крайней мере такой уровень во всей атмосфере на земле.
Это называется «средний уровень», по сути, можно говорить об уровне. На среднем уровне он записывается следующим образом. Вот почему существует функция потока, как это: ровно ноль Прямое давление. Атмосфера, это возможно с помощью уравнения Клапейрона.
Замените этот биномиал выражением. Людмила Фирмаль
В задачах теории климата (стационарных или квазистационарных задач) вблизи поверхности Земли, где контраст горизонтальных температур велик (также обусловлен существованием континентов и океанов), биномиал, приведенный здесь, является. Промежуточный уровень, где горизонтальный температурный контраст является гладким, этот биномиал не критичен для задачи бегущей волны.
Таким образом, вы можете, наконец, написать уравнение на среднем уровне. Его можно заменить только формулой и выражением, и вы получите уравнение для определения функции. Тогда доберитесь до финала.
Строго говоря, вы можете писать из любого времени: из любого времени. Поэтому уравнение удовлетворяется только на средней высоте. Как мы уже говорили в начале этого раздела, представим себе, что наше движение на среднем уровне состоит из основного, чисто зонального, западно-восточного потока, на который накладываются небольшие незональные возмущения.
Зависит только от мелких случаев. Больше где-постоянное значение. Следующий в результате это выглядит так. И затем если вставить в уравнение и отбросить его с учетом Терма, содержащего квадрат, то получится уравнение для решения Решение этого линейного уравнения можно найти в виде.
Является целым числом, неизвестной константой, неизвестной функцией. За такое решение последнее уравнение для определения. Если вы получите уравнение связанного полинома Лежандра и поместите член в квадратные скобки, равные целому числу, вы можете получить решение с границей в любом месте.
Поэтому мы приходим к отношениям где-произвольная константа. Давление определяется квадратурой. На самом деле действия атмосферы , если обратиться к уравнению, то оно получается после линеаризации (оставляя только базовую плотность среднего уровня, которая считается постоянной).
Теперь вы можете выполнить квадратурный метод и записать его следующим образом. Мы используем его и становимся равными Также обратите внимание, что вы получаете на основе того, где значение является независимым. Величина (вращательная угловая скорость основного потока) называется циклической.
Как правило, она положительна, но колеблется. По сезонам: зима, лето. Эта формула имеет ряд метеорологических. В частности, волны, наложенные на основной поток, движутся с постоянной скоростью, зависящей от индекса циркуляции и величины волны (численного значения, характеризующего величину волны).
По волнам, соответствующим малым возмущениям (большим), они движутся с запада на Восток, как бы транспортируясь к главному потоку. Напротив, большие волны движутся против валов. Мы получили членное частичное решение вида.
Таково решение гаурувии. Общее решение, которое может следовать за судьбой наложенной произвольной формы начального возмущения. Он был приобретен путем. Чтобы получить общее решение, Блинова настаивает на том, что: позволяет представить поле возмущения начального давления в виде ряда сферических функций (на среднем уровне).
С другой стороны, используя хорошо известные отношения. Здесь любое число также может быть решением системы. Теперь можно выразить через. To сделайте это, введите термин, перенумеруйте его и получите серию.
Если мы сравним ряд, в котором заданы коэффициенты, и ряд, в котором коэффициенты неизвестны для каждого члена, мы получим систему уравнений. Из этой системы уравнений коэффициенты определяются по порядку от минимума коэффициентов. Возмущение текущей функции на движение.
На практике, как показывает сравнение выражений, в случае крупномасштабных соотношений расчет упрощается. Анализ уравнения был подробно остановлен. Последнее получено в результате линеаризации уравнения. Эртер указал на возможность получения нескольких частных решений нелинейных нестационарных уравнений.
Эртель также ищет решение для вставки этих производных. После сокращения и сокращения членов происходит следующее. Итак, для любого уравнения. Решение представляет собой волну, угловая скорость которой накладывается на перенос в направлении запад-запад (как и в аналогичных решениях в случае линейного).
Угловая скорость волны выражается выражением. Но угловая скорость волны в случае линейной выглядит следующим образом: это, согласно формуле, точно совпадает с формулой, полученной в соответствующем нелинейном случае.

