Оглавление:

Теплоотдача при свободном движении в инерционных силовых полях
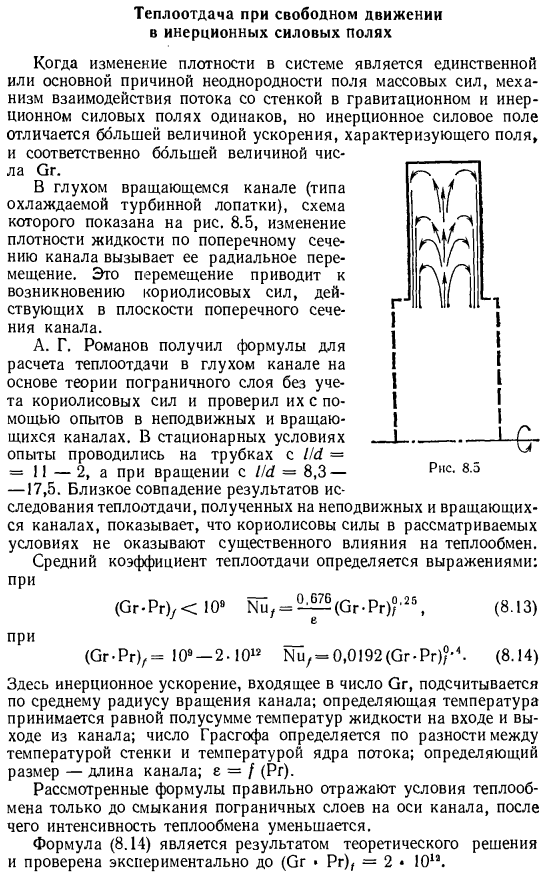
- Если изменение плотности системы является единственной или основной причиной неоднородности силового поля массы, то механизм взаимодействия потока и стенки в поле силы тяжести и инерции одинаков, но поле инерции характеризуется большим ускорением, а следовательно, и большими значениями. В глухом поворотном канале (таком как лопатка охлаждающей турбины) рисунок показан на рисунке. 8.5, изменение плотности жидкости вдоль поперечного сечения канала вызывает ее радиальное перемещение. Движение эго приводит к появлению силы Кориолиса, действующей на плоскость поперечного сечения канала. А. Г.
Локальные коэффициенты теплообмена вдоль поверхности цилиндрического тела на большем расстоянии от лобовой образующей можно также определить при помощи уравнения (7-2). Людмила Фирмаль
На основе теории пограничного слоя без учета этих сил Кориолиса Романовым получено уравнение для расчета теплопередачи в глухом канале, проверенное силовым экспериментом на стационарном и вращающемся channels. In в установившемся состоянии эксперимент проводили в трубке с II = 11-2, а при вращении с IL = 8.3-17.5.Близкое совпадение результатов исследований теплообмена, полученных в неподвижном и вращающемся каналах, свидетельствует о том, что сила Кориолиса в рассматриваемых условиях существенно не влияет на теплообмен.
- Средний коэффициент теплопередачи определяется по формуле: (О-О-РГ)0 ″ (8.13) (ОГ-РГ) г = 10 ′ −2-Yu1 детьми / −0.0192(СГ-РГ)/ (8.14). Здесь инерционное ускорение, которое входит в число 6 g, вычисляется по среднему радиусу поворота канала. Определенная температура равна половине температуры жидкости на входе и выходе канала. Число стеклопластиков определяется разницей между температурой стенки и температурой ядра потока. Определение размера-длина канала. Е = F (пр). Рассмотренная формула корректно отражает условия теплопередачи только до тех пор, пока пограничный слой не замкнется на оси канала, после чего интенсивность теплопередачи уменьшается.
Кривые значений локального коэффициента теплообмена по периметру цилиндров круглого и эллиптического сечений и по поверхности плоской плиты. Людмила Фирмаль
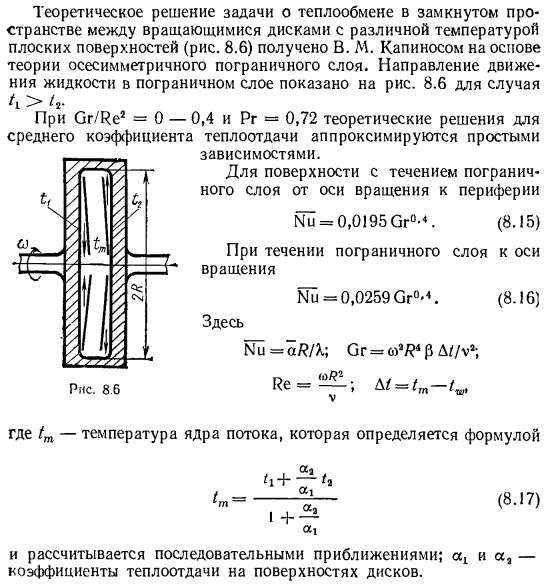
Уравнение (8.14) является результатом теоретического решения, которое экспериментально проверяется до тех пор, пока (Og•Pr)= 2•101. В. М. Капинос на основе теории осесимметричного пограничного слоя получил теоретическое решение задачи теплообмена в замкнутом пространстве между вращающимися дисками, где температура плоскости различна(рис. 8.6).Направление движения жидкости в пограничном слое показано на рисунке. 8. 6 случае 4> 4-корпус Для CG / Кэ2 = 0-0. 4 и Pr = 0,72, теоретическое решение среднего коэффициента теплопередачи аппроксимируется простым решением. Зависимости. Для ограниченных поверхностей Слои от оси вращения к периферии Г = 0.0195 л° -«.
Когда пограничный слой течет по оси II _1 * вращение 1 Jy = 0.0259 Cr0-4. (8.16) Здесь. Гг = а /?Д; СГ = О1 /?4(5 Д / М、 Рисунок 8.6 D / = / t— Где 1t-температура сердечника потока, определяемая по формуле (8.17)) Он вычисляется в последовательном приближении.
Смотрите также:
| Дополнительное условие подобия потоков в полях массовых сил | Теплоотдача в змеевиках |
| Теплоотдача при свободном движении в гравитационном поле массовых сил | Теплоотдача в закрученных потоках |

