Оглавление:
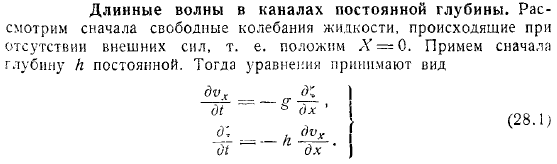

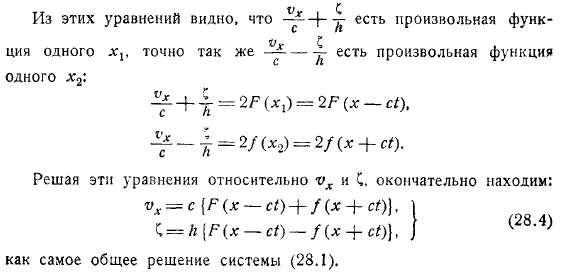




Длинные волны в каналах постоянной глубины
Во-первых, рассмотрим свободную вибрацию жидкости, которая должна быть помещена, которая возникает при отсутствии внешних сил. Сначала получите константу глубины. Уравнение принимает вид.
Например, исключите неизвестную функцию. Функция дифференцирует первое уравнение относительно и умножает первое уравнение на. Потому что получается одно и то же уравнение. Для решения уравнения введем новую независимую переменную по уравнению.
- Затем рассмотрим ее как функцию и получим по правилам дифференцирования сложные функции. И подобные выражения.
- Вставьте эти выражения в уравнение. Сформируйте сумму и разность этих уравнений и умножьте их сначала.
Из этих уравнений ясно, что существует произвольная функция. Людмила Фирмаль
Решите эти уравнения относительно. Наконец найти:как наиболее распространенное решение для системы гидромеханики. Есть также какие-либо функции. Рассмотрим частный случай упражнений.
Это легко понять физический смысл. Имеет такое же значение в геометрической точке, где координаты присутствуют в данный момент, то есть в геометрической точке, которая движется параллельно правой оси со скоростью. То же самое.
- Определенное значение распространяется параллельно правой стороне вдоль оси.
- Важно подчеркнуть Основные уравнения, что сами частицы перемещаются на очень короткие расстояния в том или ином направлении, так как частицы жидкости создают очень малые колебания. Смещение этой частицы легко вычислить.
Очевидно, равны в течение определенного периода времени. Последний интеграл, очевидно, представляет собой объем жидкости, заключенной в оси, и часть волны, проходящей через проблемное место за определенный период времени. После прохождения волны, каждая частица смещается вправо или влево.
Напротив того. Эти уравнения представляют собой распространение возмущения параллельно левой оси в то же время. Людмила Фирмаль
В общем случае уравнение представляет собой суперпозицию обеих волновых систем, причем волновая система движется вправо с одинаковой скоростью, а другие волновые системы движутся влево.
В следующей таблице показана зависимость скорости распространения длинных волн от глубины. Как показано в, потенциальная энергия волны. С другой стороны, кинетическая энергия волны четко выражается интегралом.
Вертикальная скорость в каналах переменной глубины намного меньше в горизонтальном направлении, поэтому этим термином можно пренебречь. В случае волн, распространяющихся в одном направлении, например, в правильном направлении, по формуле. Это показывает, что длинноволновая кинетическая и потенциальная энергии, распространяющиеся в одном направлении, равны.

