Оглавление:




Теплопроводность плоской стенки
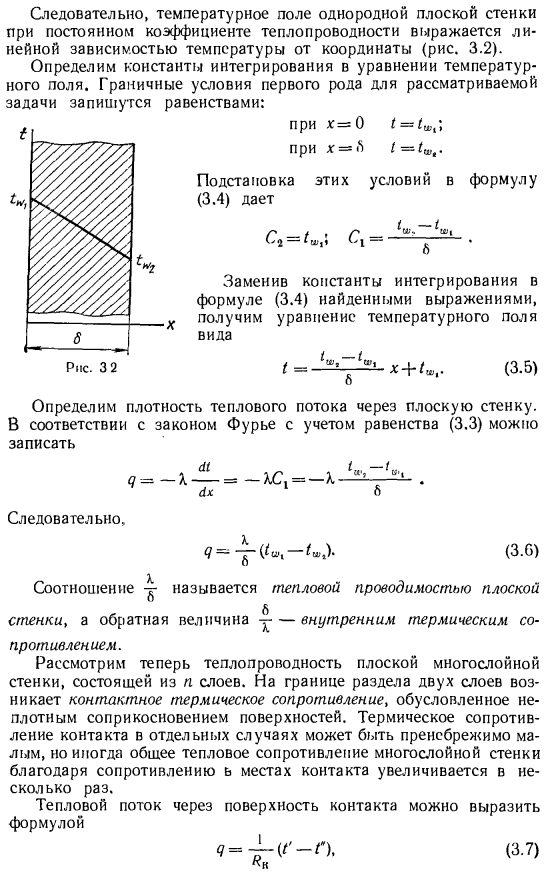
- Рассмотрим температурное поле и тепловой поток, обусловленный устойчивой теплопроводностью через плоскую, плоскую стенку, где боковая площадь очень велика и теплопередача с торцов незначительна. Часть такой стены показана на рисунке. 3.2. Толщина стенки равна 6, теплопроводность х одинакова для всей стенки, граница стенки 1А и температура изотермической плоскости в виде плоскости, параллельной стенке. В рассматриваемых условиях тепло может распространяться только вдоль оси x, и температурное поле становится одномерным. Таким образом, градиент температуры вдоль остальных осей координат равен нулю.
Дифференциальное уравнение энергии (2.15) для стационарной одномерной задачи теплопроводности плоской стенки без внутреннего источника тепла、 Если вы интегрируете это уравнение 2 раза, вы можете увидеть: (3.3) (3-4) Итак, температурное поле однородной плоской стенки с постоянной теплопроводностью представлено линейной зависимостью температуры от координат (рис.3.2). Определите константу интегрирования в уравнении температурного поля. Граничные условия вида 1, подлежащего рассмотрению Формула Определите плотность теплового потока через плоскую стенку. В соответствии с правилом Фурье, рассматривая уравнение (3.3), его можно записать следующим образом: Так…
Установление пограничного слоя вокруг передней части осесимметричного тела можно описать некоторыми модификациями, методами, описанными ранее для двухмерных пограничных слоев. Людмила Фирмаль
Отношение y называется теплопроводностью плоских стенок, а обратная величина y называется внутренним тепловым сопротивлением. Теперь рассмотрим теплопроводность плоских многослойных стенок, состоящих из n-слоев. На границе раздела между 2 слоями, контактное термическое сопротивление произведено свободным контактом поверхности. Тепловое сопротивление контактов может быть незначительным, но общее тепловое сопротивление многослойной стенки за счет сопротивления контактов может увеличиться в несколько раз. Тепловой поток через контактную поверхность может быть выражен в виде — П.、 (3.7) Где/?Контактное тепловое сопротивление*. C и I » — температура контактной поверхности.
- Изолировать температуру Поле и тепловой поток Через многослойную стенку с учетом контактного сопротивления. Толщина каждого слоя 6, и термальный коэффициент Проводимость X | (рисунок 3.3). В установившихся тепловых условиях тепловой поток через каждый слой и зону контакта становится одинаковым、 Потому что температурное поле не меняется только при этом условии Со временем. Уравнения (3.6) и (3.7) используются для представления плотности теплового потока через отдельные слои и контактные поверхности. 9= — ^- Перепишем эти уравнения в виде: Если мы суммируем правую и левую части этих уравнений、 (tG L-ISFP) 7G ’’ ISFP) Здесь — номер слоя.
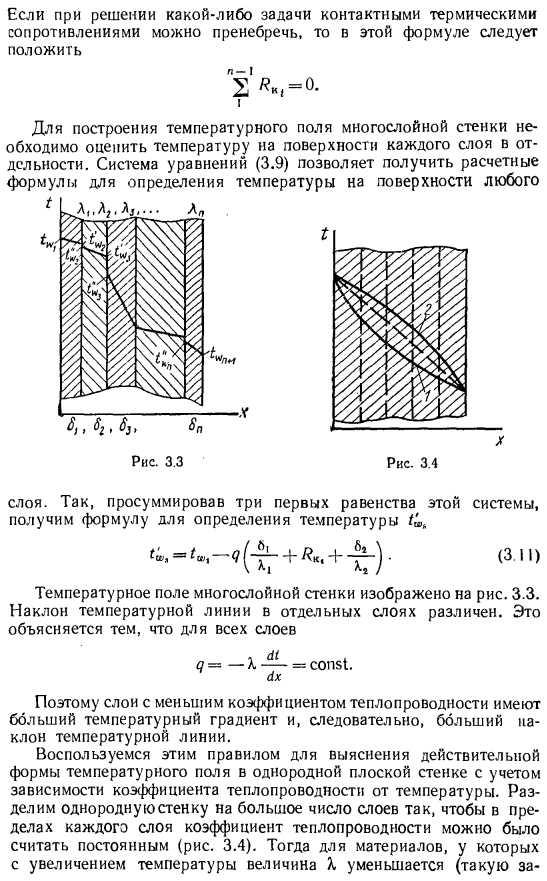
Если контактное тепловое сопротивление можно игнорировать при решении задачи, то эта формула должна включать Чтобы построить температурное поле для многослойных стен, температуру поверхности каждого слоя необходимо срезать индивидуально. Система уравнений (3.9) дает формулу для определения температуры поверхности. Рисунок 3.3 рисунок 3.4 Формула обмена мгновенными сообщениями = + +(3.11) Температурное поле многослойной стенки показано на рисунке. 3.3.Наклон температурных линий отдельных слоев различен. Это все слои 7 =- Х-Y = const1. Следовательно, чем ниже слой теплопроводности, тем больше градиент температуры и тем больше наклон температурной линии.
Эта связь между степенью турбулентности в свободном потоке и критическим числом Рейнольдса, при котором происходит падение лобового сопротивления шара, правильно истолковал Л. Людмила Фирмаль
Используя это правило, мы определяем фактическую форму температурного поля однородной и плоской стенки с учетом температурной зависимости ее теплопроводности. Разделите однородную стенку на несколько слоев так, чтобы в каждом слое теплопроводность считалась постоянной(рис.3.4).Тогда для материалов, значение X которых уменьшается с увеличением температуры (например Зависимость х от / имеет большинство металлов), в высокотемпературной зоне температурная линия идет более резко, а в низкотемпературной зоне она становится полой, чем средний коэффициент теплопроводности. Увеличение числа слоев дает кривую зависимости I в пределах limits.
Смотрите также:
| Основы теории подобия физических явлений | Теплопередача через плоскую стенку |
| Коэффициент теплопроводности λ | Теплопроводность цилиндрической стенки |

