Оглавление:



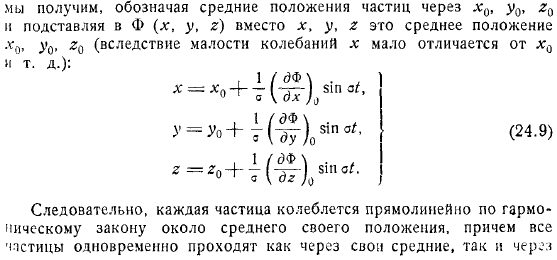



Стоячие колебания тяжелой жидкости в сосуде
До сих пор считалось, что жидкость в гидромеханике простирается бесконечно горизонтально со всех сторон. Теперь рассмотрим движение жидкости в ограниченной области, которое происходит под действием.
Примером такого движения являются так называемые Сейшельские острова озера, которые состоят из периодических колебаний уровня озера и распространяются по всему озеру. В этом разделе учитываются стационарные колебания жидкости на глубине, которая находится в цилиндрическом бассейне (в частности, если вы используете, вы получаете жидкость с бесконечно большой глубиной). Так корабельные волны, если мы возьмем начало горизонтальной плоскости, которая находится в положении равновесия, с осью, обращенной вверх вертикально, мы получим следующее уравнение дна жидкости.
- Рассмотрим невращательное движение. Потенциал скорости указан на рисунке.
- Этот потенциал скорости удовлетворяет уравнению Лапласа. Наконец, на дне и боковых стенках сосуда, состояние.
В свободной поверхности, уравнение. Людмила Фирмаль
Рассмотрим следующую форму потенциала скорости для получения стационарных колебаний жидкости. Эта формула предполагает следующую зависимость. Тогда уравнение выглядит так.
Уравнение дает связь уравнения. Период колебаний определяется простым методом. Наконец, нижняя нормаль будет соответствовать направлению оси, хотя нижнее уравнение будет заполнено самим собой.
- Остается выполнить еще одно условие боковой стенки цилиндра, ограничивающее жидкость. Сначала мы изучим полученное упражнение в общем виде.
- Скорость движения частиц жидкости определяется по формуле поэтому для интегрирования уравнения.
Получаем среднее положение частицы и подставляем среднее положение в ее положение (из-за малой вибрации оно практически не меняется). В результате каждая частица колеблется по прямой линии согласно гармоническому правилу для своего среднего положения, и все частицы проходят как через них, так и через них одновременно. Крайнее положение.
Отметим вертикальную составляющую скорости и вертикальную амплитуду. Людмила Фирмаль
Дно сосуда. кроме того, вертикальный цилиндр исчезнет во всех точках. Найти форму свободной поверхности жидкости. Таким образом, горизонтальная поверхность совершает гармонические колебания.
До определенных факторов в прямоугольном сосуде и в круговом цилиндре эта поверхность всегда принимает вид. Кривая в полости, уравнение которой имеет вид. Суть линии уровня поверхности. Их можно назвать линиями одинаковой вертикальной амплитуды, так как вертикальное движение всех частиц такой линии по формуле.
В частности, кривая является узлом вертикального движения, так как вертикальное движение частиц равно нулю. Также найдите линии тока на плоскости, которые определяются из уравнения. Как известно, это уравнение кривой, которая перпендикулярна линии уровня, и такая кривая называется линией максимального наклона.
Поэтому линии тока на плоскости являются линиями наибольшего наклона поверхности. Это условие представляет собой тот факт, что ограничивающий жидкость цилиндр проходит через обтекаемую линию в.
Дело в том, что скорость частиц, соприкасающихся с цилиндром, находится в плоскости контакта с цилиндром. Таким образом, контур поперечного сечения цилиндра по плоскости в каждой точке соприкасается с проекцией скорости на плоскость. То есть, текущая линия на плоскости.

