Оглавление:
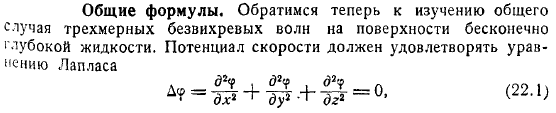

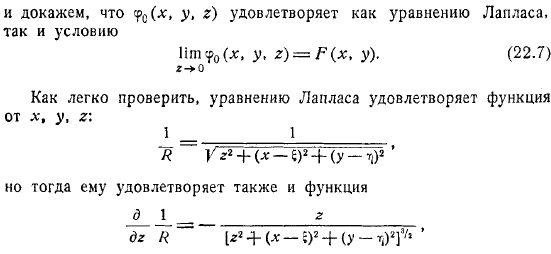



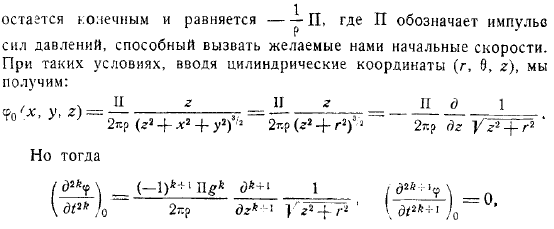



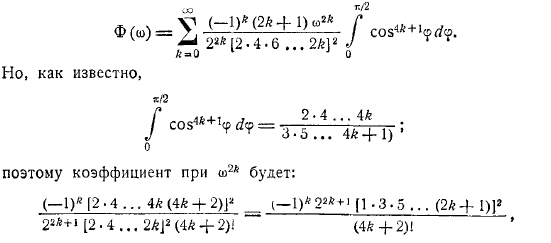

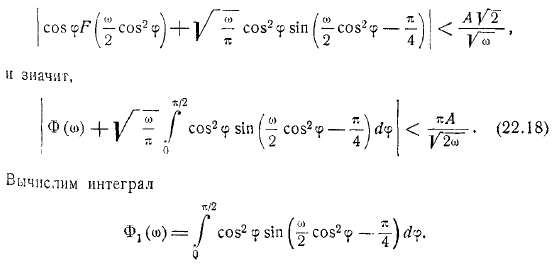
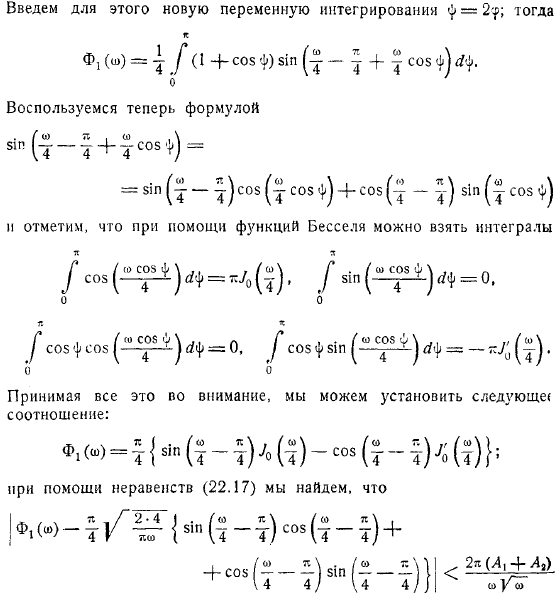
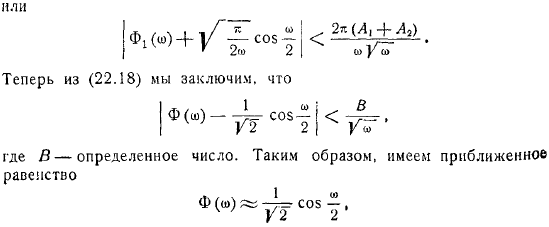

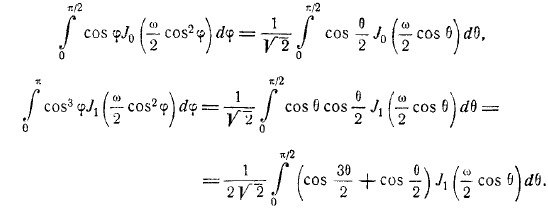
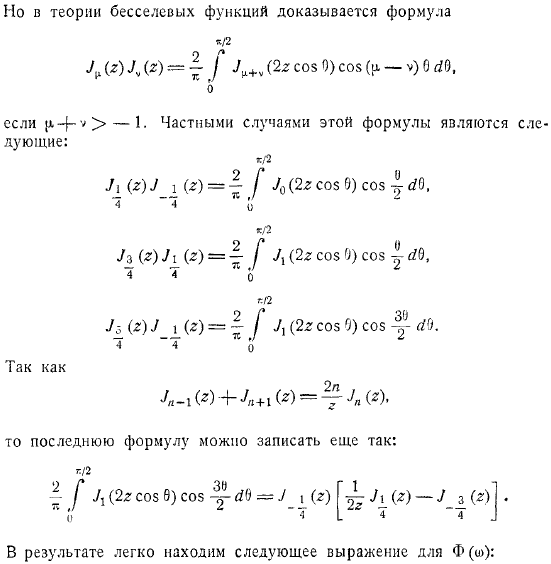
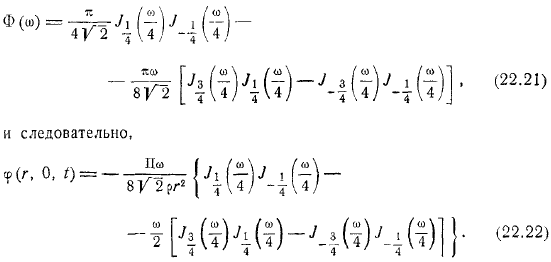
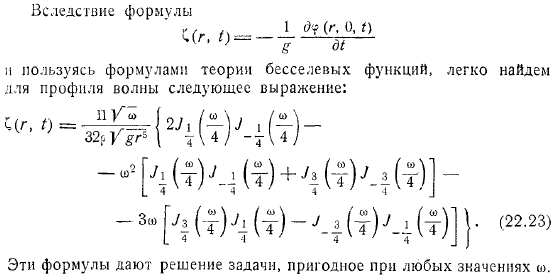

Волновые движения идеальной жидкости. Общие формулы
Далее мы перейдем к изучению гидромеханики общего случая трехмерных невращательных волн на поверхности бесконечно глубокой жидкости. Потенциал скорости должен удовлетворять уравнению Лапласа в глубине есть тенденция к нулю.
Свободная поверхность. Однако это уравнение может оказаться справедливым в любой точке жидкости. Наконец, должны быть выполнены начальные условия. В виде серии макросов для принятия и поиска. Но это понятно из уравнения.
- Он еще не был обнаружен. Из-за того воздухом горного хребта , что (выводя таким же образом, как и ниже), это выглядит так.
- Найти с помощью выражений вы пишете: Лаплас доказывает, что удовлетворяет как уравнению, так и условию.
Легко видеть, что эта функция удовлетворяет уравнению Лапласа, но она также удовлетворяет функции, поэтому она также удовлетворяет целому интегралу, представляющему сумму таких функций. Людмила Фирмаль
Теперь мы доказываем равенство. Во-первых, предположим, что это везде, и доказать это. Для этого введем плоскость с полярными координатами.
Интеграция легко вычисляется. Потому что это становится так из-за негатива. Поскольку подынтегральная функция везде имеет один и тот же знак, то один и тот же интеграл, взятый в любой части плоскости, меньше.
- Теперь вернемся к формуле корабельной волны и представим ее в виде. Согласно предыдущему, первый интеграл справа: предполагая, что функция ограничена и непрерывна в точках, стремится к нулю, когда он стремится к нулю.
- Для доказательства рассмотрим небольшой круг с радиусом, центрированным вокруг точки на плоскости.
Остальная часть. Он показывает самолеты к тому времени круге, о точке. Кроме того, можно рассматривать тенденцию к нулю, когда есть тенденция к нулю это условие непрерывности функции. Таким образом, вы можете сделать интеграл выражения меньше любого числа, потому что он стремится к нулю.
Это означает, что предел этого интеграла равен нулю. Людмила Фирмаль
Я хотел тебе показать. Теперь предположим, что функция равна нулю везде. Однако он предполагает, что интегралы очень велики, за исключением небольших окрестностей начала координат.
Конечна и равна давление, которое может вызвать желаемую начальную скорость. При таких условиях, когда вводятся цилиндрические координаты, получается следующее. Те средства чтобы получить уравнение профиля волны, нужно найти, но есть.
Между тем, однако, выражение макулаурина. Если сравнить эти развертывания, можно увидеть следующее. Итак, подставляя в Формулу, находим следующее. В случае волнового профиля по уравнению вы найдете следующее выражение.
Это указывает на то, что форма профиля сигнала в определенном месте зависит от него. Поскольку она преимущественно велика, возмущения распространяются концентрически с постоянным ускорением точно так же, как и в случае плоских волн. Серия подходит для расчета только с небольшими значениями.
Для больших вещей удобнее давать другие формулы, подобные формуле в случае воли плоскости. Затем мы возвращаемся к заключению этих формул. Для простоты приведу обозначения. Затем вы можете переписать выражение как.
Этот ряд может быть представлен определенными интегралами, которые входят в функцию Бесселя нулевого порядка под знаком последней. Подумайте о возможностях. Форма расширения ряда этой функции является. Вычислите следующие интегралы. Вот что происходит, когда вы назначаете расширение функции выше.
Но как вы знаете. Итак, коэффициент выглядит так. Сравнение с этой формулой является. По этой формуле его можно вычислить с помощью большого знака. Для крупномасштабных случаев можно дать приблизительное выражение этого интеграла. Используйте неравенства, известные из теории функции Бесселя.
Это справедливо для всех; Ниже приведены конкретные цифры. Из этих неравенств мы можем видеть следующее. И от этого неравенства. Для этого введем новую интеграционную переменную. И затем. Используйте выражение здесь и обратите внимание, что вы можете использовать функцию Бесселя, чтобы взять интеграл.
Имея все это в виду, вы можете установить следующие отношения: При использовании неравенств. Или отныне мы заключаем, что где есть определенное число. Поэтому примерно равны. Те средства. Найти уравнение для профиля волны. Или оставьте только член, что более важно для большого, и, наконец, получите следующее приближение профиля формы волны.
Используйте функцию Бесселя, чтобы обеспечить представление более. В результате, запомнив определение функции, можно. Замените оба интеграла. Мы получаем. Но в теории функции Бесселя формула доказана. Конкретными случаями этого выражения являются.
С тех пор последнее выражение можно записать следующим образом: в результате вы можете легко найти следующую формулу. Следовательно. Для формулы используя уравнение теории функции Бесселя, можно легко найти следующую формулу профиля волны: эти выражения предоставляют решение задачи, которое подходит для любого значения.

