Волны в сжимаемой жидкости. Обтекание воздухом горного хребта

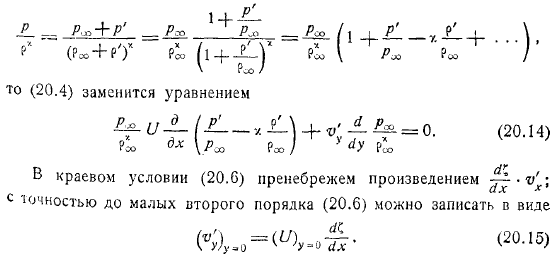
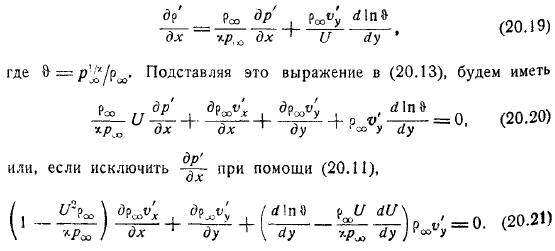
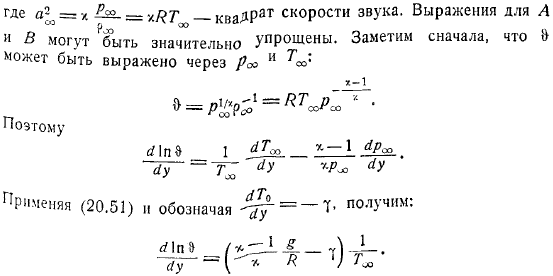
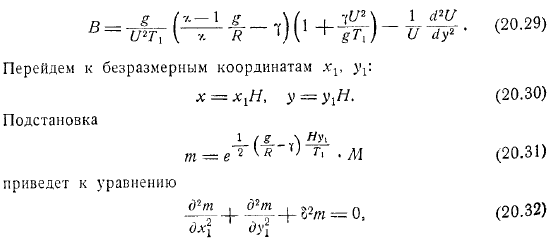
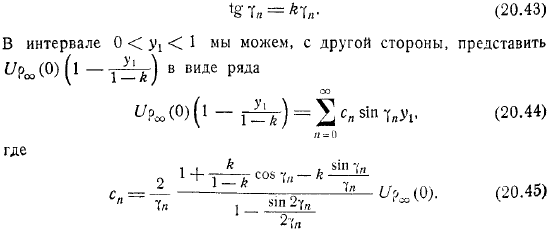
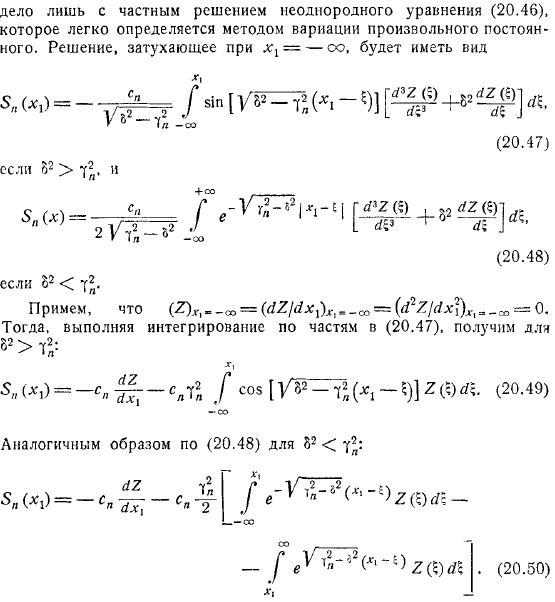
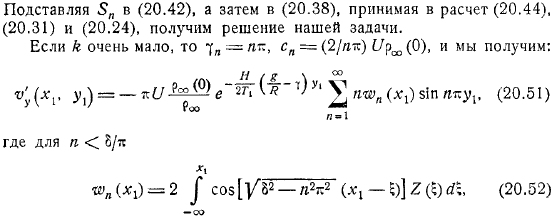
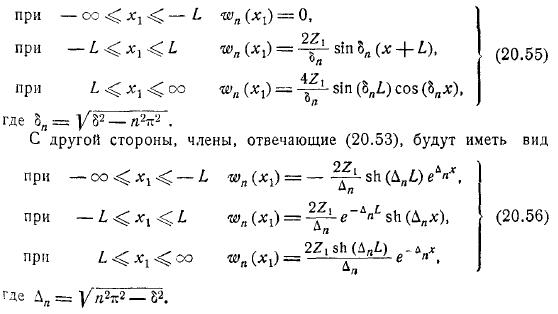
Волны в сжимаемой жидкости. Обтекание воздухом горного хребта

В предыдущем разделе гидромеханики, посвященном волне, мы ограничили ее несжимаемой. В этом разделе мы рассмотрим пример волны, создаваемой гравитацией в бароклинной сжимаемой среде. Ограничивается рассмотрением стоячих волн, возникающих при адиабатическом движении вблизи цилиндрической.

В бесконечной среде, заполненной несжимаемой жидкостью, непрерывный поток вокруг симметричного профиля вокруг оси, перпендикулярной направлению бесконечного потока, становится симметричным по отношению к этому основному. Если же, наоборот, обтекаемый профиль находится ниже свободной поверхности, то с появлением профиля волны за ней, даже в случае симметричного профиля, симметрия течения нарушается. Волны тела под свободной поверхностью, возникающие при наличии свободной поверхности, всегда имеют одинаковую длину.

• Из-за бароклинного давления возникают волны разной длины (в то же время существует конечное число таких волн). Эти волны хорошо известны облачным метеорологам, возникающим с подветренной стороны хребта.
• Детальный анализ влияния бароклинного давления впервые был дан работами дородонитина; здесь мы приводим результаты дородонитина.

И мы посмотрели на общую систему уравнений. Людмила Фирмаль

В случае стационарных задач поверхностей. Направьте ось y вверх по вертикали, а ось по горизонтали. Вы должны удовлетворить уравнения движения.

Уравнение неразрывности и уравнение притока энергии движения в адиабатические условия. Поэтому движения идеальной жидкости необходимо определить функции уравнения. Возвращается к граничному условию. Рассмотрим стабильный поток воздуха, который обтекает поверхность Земли.

• Выравнивается от поверхности до верхнего течения. Эта невозмущенная скорость потока известна как функция высоты.
• Распределение плотности по высоте непертурбативного движения в сторону от восходящей шероховатости. Известна функция высоты.

Наконец, распределение давления невозмущенного движения также известно и связано с барометрической формулой. Движение происходит в определенных полосах (струях), ширина которых равна. На верхней части этой полосы, жидкость находится в неподвижном состоянии.

Приведите уравнение шероховатости к виду. Людмила Фирмаль

Одно из граничных условий должно требовать, чтобы нормальная составляющая скорости поверхности y была равна нулю. Кроме того, на верхней границе течения при переходе из кинетической области в стационарную требуется равное давление.

Отформатируйте уравнение поверхности струи следующим образом В спокойной обстановке, есть давление. Поэтому надо писать: тип функции не известен в. Для того чтобы поверхность была поверхностью тока, необходимо требовать равенства.

Желаемый функционал представлен в следующем формате. Если нет никаких препятствий. Поскольку шероховатость и результирующее возмущение настолько малы, предположим, что определенной величиной квадрата хода можно пренебречь в любом месте.

Тогда уравнение записывается в виде. Это уравнение, если его принять во внимание, записывается следующим образом. Уравнение неразрывности выглядит следующим образом. Затем он заменяется уравнением.

Граничное условие игнорирует малое произведение точности на порядка, которое может быть записано в следующем виде. Кроме того, чтобы считаться небольшим. Если вы используете аналогичное уравнение, связанное с плотностью верхнего слоя, вы можете написать.

Вообще говоря, предполагается, что при переходе от струи к верхней среде происходит скачок плотности. Наконец примите форму если исключить его из уравнения. Таким образом, задача будет состоять в определении уравненийдо функций при граничных условиях.

Исключите все функции, кроме этой. При назначении этого выражения исключить из определения. Получить об уравнении. Где же этот звук? Выражение это может быть очень. Be первое, что нужно отметить. Применить и надписать.

Когда температура далекой струи закончится. Поток не зависит ни от высоты, ни от скорости. Постоянная, строго постоянная. При нормальных условиях в атмосфере, порядок. Таким образом, есть заказ в количестве. С другой стороны, есть заказы на количество.

Вообще говоря, он увеличивается на высоте на приблизительном расстоянии. Обычно в атмосфере присутствует порядок при этом. А содержащиеся в нем термины (и их производные) можно отбросить с большой точностью. Мы сосредоточимся больше.

По порядку величины, можно написать. Наиболее интересен случай, когда она линейно зависит от высоты и при этом практически не меняется по сравнению со своей средней. В этом случае после выполнения производной она считается постоянной и равной. И затем.

Перейдем к координатам без измерений. В уравнение. Куда? Вы можете повторить предыдущую оценку, чтобы точно рассчитать фигурные скобки как. Если показано, граничное условие принимает следующий вид. Граничное условие принимает форму новой переменной после подстановки туда и замены ее.

Из членов справа, член имеет порядок, и член имеет порядок. Значение пункта с правой стороны существенно зависит от отношения плотности перехода от верхней среды к нижней. Давление не разрушается, поэтому в нормальных условиях это соотношение близко к.

Однако, даже если вы прыгаете, если вы принимаете. Первый член справа имеет порядок, в некотором смысле. Очень точно, можно предположить. Поэтому задача состоит в решении однородных уравнений с граничными условиями (неоднородными) и (однородными).

Это будет уравнение с постоянными коэффициентами, решение которого можно легко получить. Введем вспомогательную функцию из уравнения функция удовлетворяет уравнению неравномерного. И однородные граничные условия. Я ищу решение следующего формата удовлетворяет.

Для того чтобы выполнить условия, необходимо принять решение из отношений. В то же время, вы можете: если мы вставим член в член, то получим следующее. Обыкновенное дифференциальное уравнение. В интересном для погоды случае значение значительно меньше.

Если вы принимаете, мы получим. Это означает, что корни трансцендентального уравнения близки к корням уравнения и могут быть рассмотрены. Если эти продукты не соответствуют вашим потребностям, пожалуйста, свяжитесь с нами, и мы хотели бы предоставить соответствующую информацию, например, когда мы получим.

То есть коэффициент первых нескольких значений будет положительным, но начиная с определенного числа, он будет отрицательным. Это существенное различие между сжимаемой бароклинной атмосферой и несжимаемой жидкостью. Последнее можно получить, официально поверив.

Но тогда она определяется, как и раньше. Где. Теперь, чтобы быть позитивным, вам нужно иметь чисто образное воображение. Это дает уравнение, и если да, то есть только одно решение этого уравнения. Решение практически. В первом случае приходится иметь дело с периодическими.

В обоих случаях решение однородного уравнения должно быть. В первом случае, согласно смыслу задачи, поскольку возмущение далеко опережает препятствие, во втором случае решение является. Вам нужно иметь.

Это лишь частичное решение уравнения с неоднородностью, которое легко определяется изменением любой константы. Раствор, подлежащий разложению, имеет вид. Принять его. Затем выполнить интегрирование по частям.

Аналогично подставьте, а потом учтите и получите решение проблемы. Если он очень маленький, вы получите. Также найдите уравнение потока. Предположим, что речь идет об обтекаемой линии на крайней левой высоте препятствия.

Уравнение для такой линии потока выглядит следующим образом: После этого вы можете написать. Отсюда, до маленького (малого), он выглядит так. Чтобы лучше понять структуру потоков, рассмотрим простой пример. Сделайте так, чтобы препятствия имели прямоугольную форму в плоскости сечения.

Затем укажите члены формы. Можно видеть, что элемент типа быстро распадается как с наветренной, так и с подветренной стороны. Легко видеть, что в этом случае эти члены симметричны относительно оси препятствия, и они вносят свой вклад в схему течения симметрично относительно оси.

И наоборот, член типа (небольшое число) не возмущается с наветренной стороны, но вызывает периодические возмущения, которые не затухают с подветренной стороны. Эти возмущения называются волнами с подветренной стороны.

Такое возмущение часто приводит к образованию параллельных гребней облаков самопроизвольно за гребнями (при положительных вертикальных течениях возникают дополнительные условия для конденсации влаги и образования облаков;при нисходящем течении и уменьшении облачности), а также к тем, которые не движутся, несмотря на сильные вертикальные ветры .

Мы. Не существует типа волны, и все решения имеют свои особенности. Волна с подветренной стороны. В общем случае, если это зависит от высоты, кривизна становится важной профиль скорости. Если у вас есть. Опять же; наоборот, если он достаточно велик. Когда-нибудь.