Оглавление:
Прогнозирование методом экспоненциального сглаживания
Вначале введем понятие экспоненциальной средней. При вычислении скользящих средних — простой и взвешенной — всем уровням динамического ряда присваивались одинаковые веса. Вес отдельного наблюдения указывает на часть вклада его значения в значение средней. В случае простой скользящей средней эта часть равна 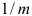 для наблюдений, входящих в среднюю, и нулю для наблюдений, отсутствующих в ней. При этом недавние данные имеют тот же вес, что и данные, относящиеся к далекому прошлому (старые). Однако понятно, что недавние данные имеют более важное значение и должны иметь больший вес. Поэтому предлагается процедура усреднения с разными весами. При этом система весов образует ряд, в котором веса убывают во времени по экспоненциальному закону:
для наблюдений, входящих в среднюю, и нулю для наблюдений, отсутствующих в ней. При этом недавние данные имеют тот же вес, что и данные, относящиеся к далекому прошлому (старые). Однако понятно, что недавние данные имеют более важное значение и должны иметь больший вес. Поэтому предлагается процедура усреднения с разными весами. При этом система весов образует ряд, в котором веса убывают во времени по экспоненциальному закону:
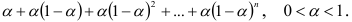
Сумма этого ряда стремится к единице при неограниченном увеличении числа слагаемых.
Используя экспоненциально взвешенные веса, экспоненциально взвешенную среднюю первого порядка будем вычислять по формуле
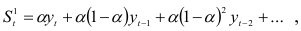
которую можно преобразовать к виду:
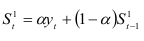
На основе этого уравнения строятся другие модели экспоненциального сглаживания.
Иногда при построении моделей прибегают к вычислению экспоненциально взвешенных средних более высоких порядков, т.е. средних, получаемых путем многократного экспоненциального сглаживания. Такая средняя вычисляется по формуле:
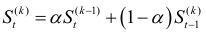
Из этой формулы легко получаются выражения:
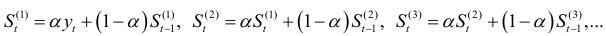
Экспоненциально взвешенная средняя имеет ряд преимуществ перед традиционной скользящей средней.
- Для вычисления экспоненциально взвешенной средней
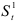 используется предыдущая экспоненциально взвешенная средняя
используется предыдущая экспоненциально взвешенная средняя 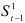 , и последнее значение уровня
, и последнее значение уровня 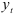 .
. - Для построения прогноза по экспоненциально взвешенной средней необходимо задать начальную оценку прогноза. При поступлении новых данных прогнозирование можно продолжать незамедлительно, т.е. нет необходимости заново строить процедуру вычисления прогноза.
- В экспоненциально взвешенной средней значения весов убывают со временем, т.е. нет такой точки, на которой веса обрываются.
Метод экспоненциально взвешенной средней разработан для анализа динамических рядов, состоящих из большего числа наблюдений. Поэтому, если динамические ряды слишком короткие (15-20 уровней) и в случае, когда темпы роста и прироста велики, метод не «успевает» отразить все изменения. Метод тем точнее, чем больше число наблюдений (уровней динамического ряда).
Рассмотрим теперь, как применяется метод экспоненциально взвешенной средней при прогнозировании экономических показателей.
Предположим, что динамический ряд представлен в виде
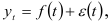
где 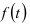 — тренд;
— тренд; 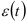 — случайная компонента. Если на изучаемом интервале времени коэффициенты уравнения, описывающего тренд, остаются неизменными, то для построения модели прогноза можно использовать метод наименьших квадратов. Однако в течение анализируемого периода коэффициенты уравнения тренда изменяются во времени. И так как динамические ряды, характеризующие экономические процессы, содержат небольшое число уровней, применение метода наименьших квадратов для оценки параметров модели прогноза может привести к существенным ошибкам. Поэтому применяется метод экспоненциально взвешенной средней, в котором новым данным придаются большие веса, чем старым.
— случайная компонента. Если на изучаемом интервале времени коэффициенты уравнения, описывающего тренд, остаются неизменными, то для построения модели прогноза можно использовать метод наименьших квадратов. Однако в течение анализируемого периода коэффициенты уравнения тренда изменяются во времени. И так как динамические ряды, характеризующие экономические процессы, содержат небольшое число уровней, применение метода наименьших квадратов для оценки параметров модели прогноза может привести к существенным ошибкам. Поэтому применяется метод экспоненциально взвешенной средней, в котором новым данным придаются большие веса, чем старым.
Пусть тренд определяется линейной функцией 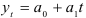 . Как показал Р.Г. Браун, оценки коэффициентов
. Как показал Р.Г. Браун, оценки коэффициентов 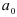 и
и 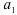 выражаются через экспоненциально взвешенные средние по формулам:
выражаются через экспоненциально взвешенные средние по формулам:
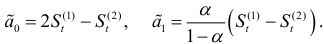
Прогноз для случая, когда тренд характеризуется линейной функцией, вычисляется по формуле
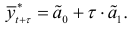
Чтобы воспользоваться формулой (9.9) для прогнозирования, нужно определить значения параметров 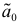 и
и 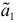 которые выражаются через экспоненциально взвешенные средние. А из формул (9.7) и (9.8) следует, что для вычисления
которые выражаются через экспоненциально взвешенные средние. А из формул (9.7) и (9.8) следует, что для вычисления 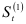 и
и 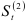 необходимо задать начальные значения
необходимо задать начальные значения 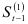 и
и 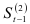 или в общем случае
или в общем случае 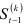 , которые будем называть в дальнейшем начальными условиями.
, которые будем называть в дальнейшем начальными условиями.
Начальные условия либо задают исходя из экономических соображений (например, из величины лага), либо вычисляют по формулам:

В качестве значений коэффициентов 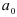 и
и 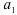 нужно брать коэффициенты уравнения тренда, полученные методом наименьших квадратов, т.е. найденные при решении системы
нужно брать коэффициенты уравнения тренда, полученные методом наименьших квадратов, т.е. найденные при решении системы
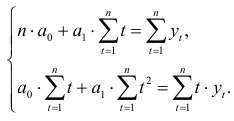
Затем вычисляются экспоненциально взвешенные средние первого и второго порядков:
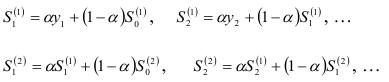
Ошибка прогноза при использовании доверительного интервала (9.3) определяется по формуле
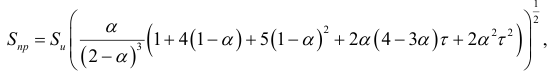
где 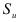 — средняя квадратичная ошибка, характеризующая отклонения от линейного тренда:
— средняя квадратичная ошибка, характеризующая отклонения от линейного тренда:
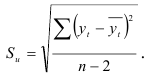
При использовании прогностической модели (9.10) одной из основных проблем является выбор оптимального значения параметра сглаживания 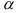 , где
, где 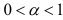 . От численного значения
. От численного значения 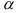 зависит, насколько быстро будет уменьшаться вес предшествующих наблюдений, т.е. насколько быстро будет уменьшаться степень их влияния на сглаженный уровень. Это значит, что чувствительность экспоненциально взвешенной средней в целях повышения адекватности прогностической модели может быть в любой момент изменена путем изменения значений
зависит, насколько быстро будет уменьшаться вес предшествующих наблюдений, т.е. насколько быстро будет уменьшаться степень их влияния на сглаженный уровень. Это значит, что чувствительность экспоненциально взвешенной средней в целях повышения адекватности прогностической модели может быть в любой момент изменена путем изменения значений 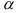 . Чем больше
. Чем больше 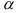 , тем выше чувствительность средней. Чем меньше значение
, тем выше чувствительность средней. Чем меньше значение 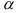 , тем устойчивее становится экспоненциально взвешенная средняя. Если подходящими оказываются более высокие значения а, это указывает на нарушение условий стационарности и означает, что экспоненциально взвешенная средняя становится неприемлемой для прогнозирования. Значения
, тем устойчивее становится экспоненциально взвешенная средняя. Если подходящими оказываются более высокие значения а, это указывает на нарушение условий стационарности и означает, что экспоненциально взвешенная средняя становится неприемлемой для прогнозирования. Значения 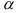 при условии равенства среднего значения степени старения данных можно выбирать, используя формулу:
при условии равенства среднего значения степени старения данных можно выбирать, используя формулу:
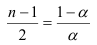
или
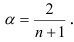
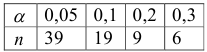
Значения 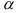 , используемые в области экономического прогнозирования, находятся в пределах от 0,05 до 0,3. Длина усреднения в скользящем среднем с точки зрения чувствительности прогноза может быть найдена в соответствии с
, используемые в области экономического прогнозирования, находятся в пределах от 0,05 до 0,3. Длина усреднения в скользящем среднем с точки зрения чувствительности прогноза может быть найдена в соответствии с  из таблицы
из таблицы
Достоинство метода экспоненциально взвешенной средней по сравнению с другими методами состоит в его точности, которая увеличивается с увеличением числа уровней динамического ряда. Но остается нерешенной проблема выбора оптимального значения параметра сглаживания 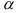 и начальных условий. Точность прогноза по этому методу падает с увеличением горизонта прогнозирования.
и начальных условий. Точность прогноза по этому методу падает с увеличением горизонта прогнозирования.
Пример 9.4.
Рассмотрим динамический ряд, характеризующий производство цемента (таблица 9.4)
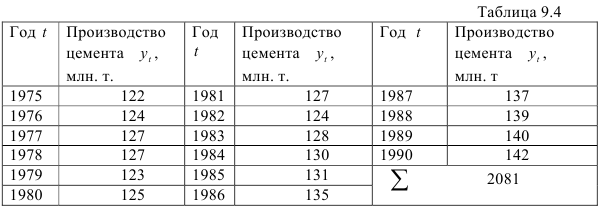
Для построения тренда
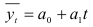
описывающего динамический ряд, начало координат было перенесено в середину ряда. Тогда система нормальных уравнений для оценки параметров тренда упрощается:
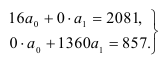
Решая ее, находим:
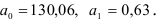
уравнение тренда имеет вид:
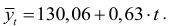
Для прогноза выпуска цемента на 1991 г. воспользуемся формулой (9.10). Оценки коэффициентов 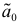 и
и 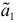 найдем из выражений:
найдем из выражений:
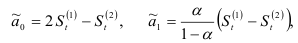
которые содержат экспоненциально взвешенные средние 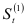 и
и 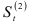 и параметр
и параметр 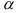 . Параметр сглаживания а положим равным 0,15, так как для
. Параметр сглаживания а положим равным 0,15, так как для 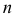 = 19 рекомендуется брать
= 19 рекомендуется брать 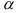 = 0,1; в нашем примере
= 0,1; в нашем примере 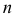 = 16. Вычисление
= 16. Вычисление 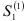 и
и 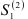 осуществим по рекуррентной формуле (9.9), предварительно определив начальные условия
осуществим по рекуррентной формуле (9.9), предварительно определив начальные условия 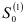 и
и 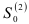
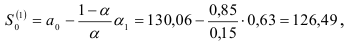
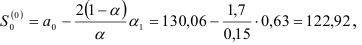
где, 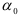 и
и 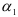 — коэффициенты уравнения тренда. Тогда:
— коэффициенты уравнения тренда. Тогда:
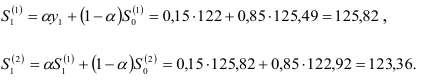
Затем вычисляем 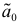 и
и 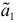
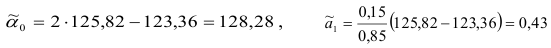
и осуществляем прогноз на 1976 г. Далее по рекуррентной формуле (9.9) вычисляем новые 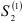 и
и 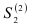 :
:
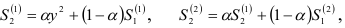
и по ним находим 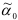 и
и 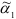 которые используем для прогноза производства цемента на 1977 г., и т.д. В таблице 9.5 приведены:
которые используем для прогноза производства цемента на 1977 г., и т.д. В таблице 9.5 приведены:
- экспоненциально взвешенные средние, вычисленные по формуле (9.9); -соответствующие коэффициенты
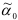 и
и 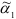 ;
;
результаты прогноза и отклонения фактических уровней от прогнозируемых в случае ретроспективного прогноза;
- указан прогноз производства цемента на 1991 г.
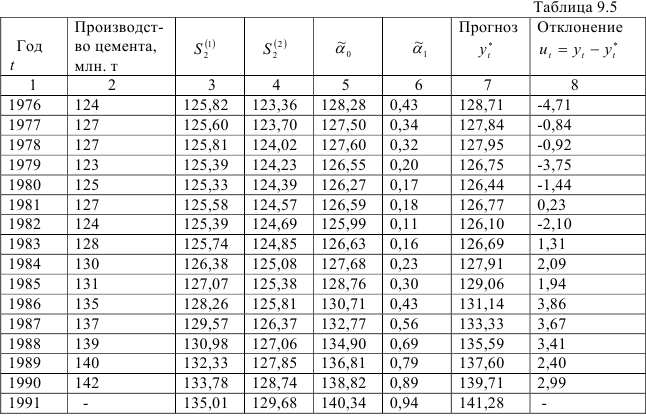
Для прогноза производства цемента на 1991 г. использовались следующие значения экспоненциально взвешенных средних:
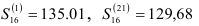
и оценки коэффициентов модели
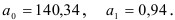
Ошибку прогноза вычислим по формуле
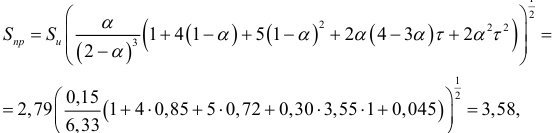
где средняя квадратичная ошибка
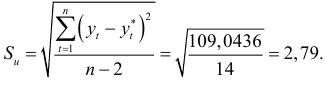
Тогда доверительный интервал прогноза определяется в виде (9.3), где  квантиль распределения Стьюдента при уровне доверия
квантиль распределения Стьюдента при уровне доверия  = 0,1 и числе степеней свободы к
= 0,1 и числе степеней свободы к 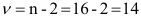 , равный
, равный 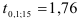 . Подставив значения
. Подставив значения 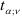 и
и 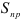 получим доверительный интервал прогноза
получим доверительный интервал прогноза
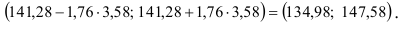
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

