Оглавление:
Методы определения сезонных колебаний
Одной из задач анализа динамических рядов является задача обнаружения определенных закономерностей, которые регулярно повторяются с периодом, равным двенадцати месяцам (или нескольким месяцам), и называются сезонными колебаниями. В общем случае сезонными колебаниями будем называть все такие изменения динамического ряда, которые соответствуют одинаковому и строго периодическому ритму в определенной причинной связи, если период ритма и не равен одному году.
Исследование сезонности предполагает выявление и измерение периодических колебаний в рядах динамики, выявление факторов, вызывающих сезонные колебания, и определение экономических последствий проявления сезонности.
Сезонная компонента находится путем исключения из данных всех других компонент и вычисляется для каждого месяца (или сезона) года, как правило, в виде индекса.
При анализе сезонных колебаний следует учитывать тот факт, что период колебаний равен одному году (нескольким месяцам) и что наблюдения обычно проводятся лишь через определенные интервалы: ежеквартально, ежемесячно, еженедельно. Большинство выводов, относящихся к сезонным колебаниям в течение года, может быть адекватно распространено и на циклические процессы с иным периодом времени. Примером может служить изменение температуры в течение дня или цен в течение недели.
Разработано несколько способов исследования сезонных колебаний: простой средней, скользящей средней (простой и взвешенной), относительных чисел. Наиболее точным, а, следовательно, наиболее распространенным является метод расчета сезонных волн, базирующийся на определении тенденции с помощью скользящей средней и методом наименьших квадратов.
Считая, что влияние сезонности носит мультипликативный характер, рассмотрим модель вида
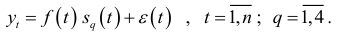
Использование этой модели заключается в выделении сезонной компоненты делением уровней динамического ряда на среднее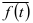 
тренда по рассматриваемому году. Полученные отношения рассматриваются как опенки мультипликативного сезонного фактора.
Разделив поквартальные величины на эти средние, получим показатели сезонности. Для определения индексов сезонности, характеризующих сезонную компоненту, вычисляем средние поквартальных данных.
Иной подход заключается в предварительном исключении тренда методом скользящих средних и последующем изучении остаточных характеристик сезонности. Если, при этом, простая скользящая средняя с равными весами вычисляется по отрезку длиной, равной периоду циклической компоненты, то значение тренда для этой компоненты равно нулю. Следовательно, остаток остается незатронутым.
Исключение тренда иногда производят, осуществляя более тщательное скользящее усреднение. Для этого вычисляют взвешенные скользящие средние, производя выравнивание интервала сглаживания полиномом некоторой степени.
Если уровни динамического ряда характеризуют экономический процесс по месяцам, то определение сезонной компоненты начинается с расчета 12-месячной скользящей средней. Так как сезонные колебания имеют постоянный период в 12 месяцев, этим методом можно пользоваться с большей уверенностью, чем в случае, когда изучается цикл с неопределенным периодом. Поскольку отдельные наблюдения подвержены влиянию случайных факторов, то размер колебаний непостоянен из года в год. Поэтому уровень, вычисленный с помощью скользящей средней, не полностью свободен от сезонных влияний и отклонения от него представляют сезонные колебания не точно. Чтобы частично устранить эти погрешности, будем вычислять индексы сезонных изменений по скользящим средним: как средние отношения эмпирических месячных данных к скользящему уровню по месяцам. Вычисляемая скользящая средняя должна относиться к тому самому моменту, к которому относится соответствующий сопоставимый с ней первоначальный уровень. Для выполнения этого требования нужно вычислить среднее из двух скользящих средних, т. е. произвести центрирование.
Например, помесячные данные должны быть отнесены к середине каждого месяца. Среднее из 12 помесячных данных для некоторого года приходится на 1 июля. Среднее из 12 уровней, начиная с февраля этого года и до января следующего года, приходится на 1 августа. Поэтому для получения уровня, который можно сравнить с исходным отнесенным к 15 июля, вычисляем среднее из этих двух средних. Таким образом, сохраняется сопоставимость ряда скользящих средних с исходным динамическим рядом.
Для вычисления точного индекса, характеризующего высоту сезонной волны для каждого месяца года, применяются различные методы. Но наиболее подходящими показателями такого индекса будут средняя арифметическая и медиана. Необходимо производить выправление средней арифметической и медианы, так как их среднее значение за 12 месяцев редко равно 100, потому что трудно добиться полного исключения влияния несезонных факторов. Для выправления среднего арифметического по месяцам нужно каждую помесячную среднюю арифметическую умножить на обратную величину средней арифметической за 12 месяцев. После такого выправления, среднее, из выправленных средних арифметических, будет равно 100. Аналогичное выправление производится и для медианы. Отметим, что вычисленная таким образом средняя арифметическая реагирует на все происходящие изменения, поэтому может быть искажение под влиянием необычных событий. Медиана же не подвержена влиянию колебаний в отдельные месяцы. Она будет значительно изменяться, если помесячные данные распределения численностей не являются концентрированными.
Для того чтобы оценить сезонную компоненту в аддитивной модели, нужно также вначале оценить тренд. Скользящая средняя с равными весами, вычисляемая на отрезке усреднения, равном одному году, не должна сильно повлиять на остатки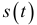 
.
Рассмотрим динамический ряд с месячными данными. Будем вычислять центрированные скользящие средние по формуле
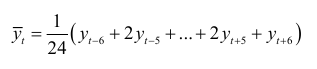
и налагать то же ограничение, что и для аддитивной модели:
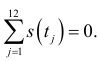
Суть этого ограничения состоит в том, что простая скользящая средняя, которая, как правило, оценивает линейный тренд, в этом случае фактически элиминирует полином 2-го порядка. Более того, средняя, которая элиминирует полином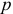 
-го порядка при ограничении 
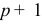, будет элиминировать полином порядка 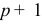. Вычисляя скользящие средние, мы тем самым вычисляем значения тренда. Но, как указал Д.Дарбин, определение значений тренда для выявления сезонных колебаний не является необходимым. Покажем это. Обозначим через 
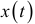отклонения уровней динамического ряда от 12-месячной скользящей средней:
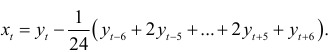
Вычислим средние отклонений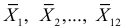 
:
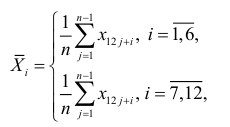
где число уровней динамического ряда равно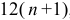 
, а не 
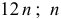— число лет. Различные пределы суммирования объясняются тем, что центрированная 12-месячная средняя дает первое значение для седьмого уровня динамического ряда, а последняя — для 
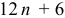. Сезонный эффект определим как разность, т. е.
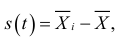
где
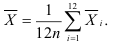
Определив месячные средние исходного динамического 12 ряда по формуле
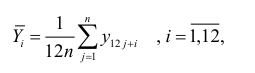
а общую среднюю, не считая шести первых и шести последних значений, по формуле
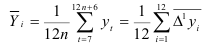
и подставив полученные значения в выражение (7.3), будем иметь
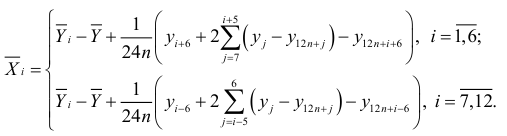
Отсюда следует, что значения отклонений от тренда могут быть получены по месячным средним без построения тренда. Необходима только корректировка, использующая первые и последние двенадцать членов ряда. Значения остальных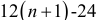 
уровней динамического ряда учитываются через месячные средние. Указанный метод определения сезонных колебаний эффективен, так как оценки месячных сезонных эффектов, полученные по 
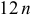значениям без элиминирования тренда, имеют дисперсию, равную:
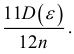
Оценка несезонной постоянной, которая является составляющей в рассматриваемом методе, имеет дисперсию, не меньшую
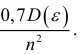
Рассмотрим теперь динамический ряд, состоящий из квартальных данных за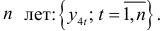 
Отклонения от тренда данных за первый квартал равны:
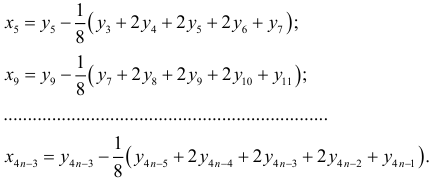
Их сумма равна:
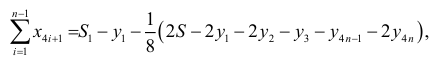
где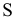 
— сумма всех уровней динамического ряда, 
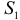— сумма уровней первого квартала. Аналогично определяются суммы отклонений для остальных трех кварталов:
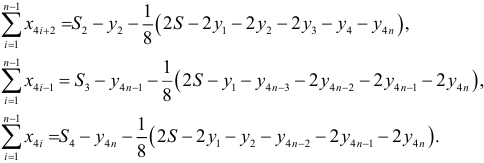
Так как
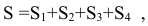
то среднее значение этих сумм равно:
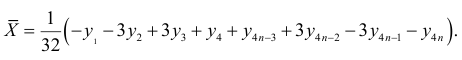
Индексы сезонности определим вычитанием этой средней из сумм отклонений, вычисленных для каждого квартала. Они будут равны:
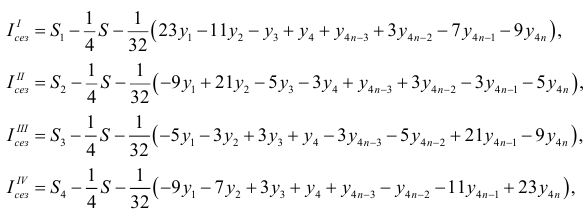
Следовательно, индексы сезонности равны отклонениям квартальных средних от общей средней, скорректированных членами, зависящими только от первых четырех и последних четырех значений динамического ряда.
Определив основную тенденцию динамического ряда методом скользящих средних и выбрав форму кривой тренда, с помощью метода наименьших квадратов оценивают параметры кривой тренда. Затем для каждого квартала или месяца рассматривают отношение фактического уровня к показателю, вычисленному по уравнению тренда. Тем самым получают показатели сезонности. Индексы сезонности рассчитываются по способу средней арифметической из показателей сезонности. Далее производится выправление индексов сезонности. Индексы сезонности можно вычислять и по расположению. Для этого в ранжированном ряду показателей сезонности для каждого квартала отбрасываются наибольшие и наименьшие значения. Для оставшихся значений показателей вычисляется средняя арифметическая. Такая средняя арифметическая по расположению не подвержена влиянию крайних значений, следовательно, индексы сезонности более устойчивы.
После определения индексов сезонности по месяцам или кварталам определяют уровни динамического ряда, в которых элиминировано влияние сезонности. Для этого необходимо фактические уровни динамического ряда разделить на соответствующие индексы. Затем снова методом наименьших квадратов оценивают параметры уравнения тренда.
Показателем колеблемости динамического ряда за счет сезонности является среднее квадратичное отклонение, определяемое по формуле
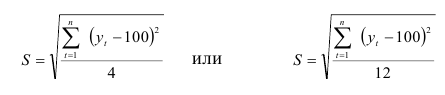
для поквартальных или месячных данных соответственно.
Пример 7.4.
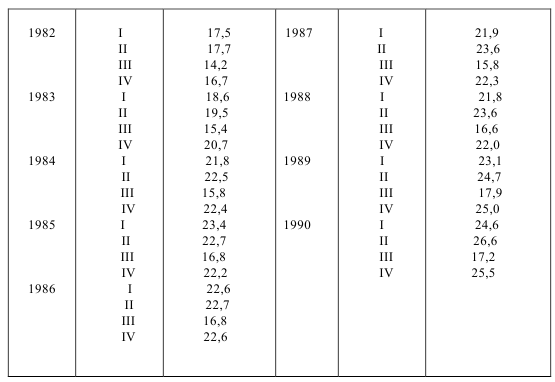
В табл.7.5 приведены данные об объеме ежеквартальных продаж в фирме »Квант», производящей сельскохозяйственный инвентарь.
Исследование сезонности проведем методом, базирующимся на определении тенденции методом наименьших квадратов и определении индексов сезонности, рассчитанных по уравнению тренда.
Определим уравнение тренда исследуемого динамического ряда. Для этого вычислим средние скользящие приросты по формуле
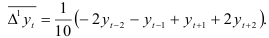
Так как средние скользящие приросты примерно одинаковы, то для исследуемого динамического ряда характерен линейный тренд
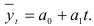
Параметры тренда оценим, решив систему:
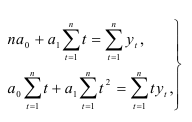
которую предварительно упростим, перенеся начало координат в середину ряда динамики. После этого параметры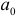 
и 
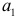определим по формулам:
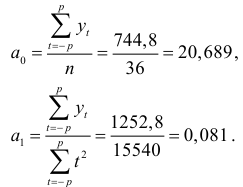
Итак, искомое уравнение тренда имеет вид
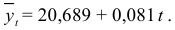
Затем определим расчетные уровни по уравнению тренда. Индексы сезонности являются показателями, характеризующими результаты сравнения фактических уровней данного квартала с уровнями, вычисленными при выявлении тенденции для этого же квартала. Индексы сезонности определим двумя способами: исключив тренд, во-первых, с помощью центрированных скользящих средних:
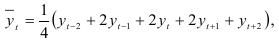
во-вторых, с помощью уравнения
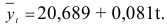
Исключив тренд с помощью центрированных скользящих средних или уравнения
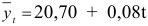
и получив показатели сезонности, вычислим среднюю арифметическую из них по одноименным кварталам, т.е. определим индексы сезонности. В табл. 7.6 приведены вычисленные таким образом индексы сезонности для каждого квартала. Полное элиминирование несезонных факторов достигается тогда, когда средняя из индексов сезонности равна 4. В нашем случае сумма индексов сезонности, вычисленных с помощью скользящих средних, равна 4,004, а с помощью уравнения тренда — 3,996. Поэтому произведем выправление индексов сезонности. Для этого разделим их на 1,001 и 0,999 соответственно.
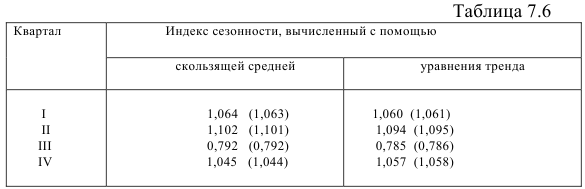
В скобках указаны выправленные индексы.
Сравнив соответствующие индексы сезонности с выправленными индексами, видим, что расхождение между ними небольшое. Это объясняется тем, что сезонные колебания относительно невелики и повторяются из года в год. Анализируя данные табл. 7.6, замечаем, что »сезонный пик» продаж достигается во втором квартале, а «сезонная яма» — в третьем. Этот факт подтверждается индексами сезонности, вычисленными с помощью скользящей средней и с помощью уравнения тренда.
Исключив сезонность из уровней ряда динамики, оценим параметры и тренда
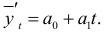
Выполнив промежуточные расчеты, найдем:
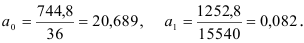
Таким образом, уравнение тренда
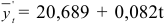
отличается только коэффициентом при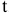 
. Этот факт еще раз подчеркивает влияние сезонности на уровни продаж.
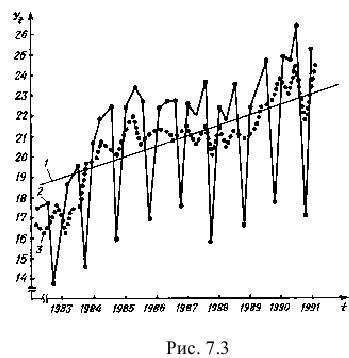
График тренда, уровни исходного динамического ряда и уровни ряда после исключения сезонности представлены на рис. 7.3 (линии 1-3 соответственно). Исключив сезонные колебания, из графика замечаем, что на скорректированные уровни динамического ряда, кроме тренда, оказывают влияние еще циклическая и случайная компоненты.
Для исследования периодических колебаний в рядах динамики целесообразно применять гармонический анализ.
Если величину изучаемого показателя 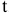представить как части длины окружности:
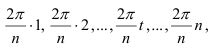
где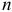 
-число значений изучаемого показателя или величина периода, то зависимость соответствующих им значений уровней динамического ряда запишется в виде следующей суммы:
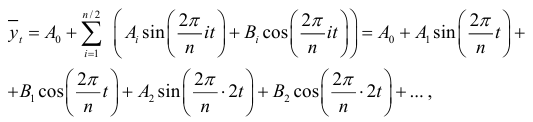
которая представляет собой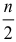 
гармоник ряда Фурье.
Практически выявление периодичностей состоит в преобразовании исходной тенденции в новую тенденцию, где роль периодической компоненты проявляется ярче. Задача, таким образом, сводится к аппроксимации тенденции суммой (7.5), в которой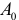 
— среднее значение за период; 
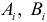— неизвестные коэффициенты гармоник. Коэффициенты 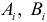оцениваются по методу наименьших квадратов, т. е. при условии минимизации функции
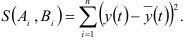
Получение формул для коэффициентов облегчается благодаря свойству ортогональности:
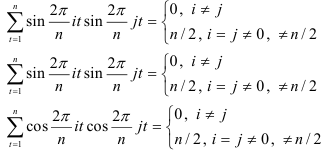
Тогда минимум функции (7.6) достигается при следующих значениях коэффициентов
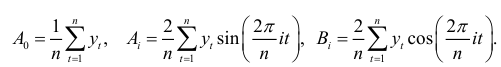
Так как число гармоник не может превышать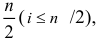 
то по этим формулам вычисляются коэффициенты для 
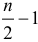гармоник. Для последней гармоники всегда
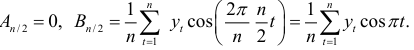
Если вычислять число гармоник и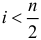 
, то число коэффициентов при синусах и косинусах будет одинаковым.
Уравнение (7.5) называется амплитудным и фазовым представлением тенденции, а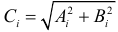 
амплитудой. Дисперсия, учитываемая одной гармоникой, определяется по формуле 
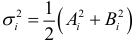. Для последней гармоники 
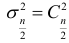. Часть дисперсии, учитываемая определенной гармоникой, представляется в виде отношения величины 
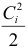или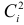 
к общей дисперсии 
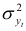. Так как никакие две гармоники не между собой, то они не будут учитывать одну и ту же часть общей дисперсии, т. е. дисперсии, учитываемые различными гармониками, складываются.
Пример 7.5.
Применим гармонический анализ для расчета периодической функции для динамического ряда, характеризующего реализацию товаров весенне-летнего сезона (данные приведены в табл . 7.7).
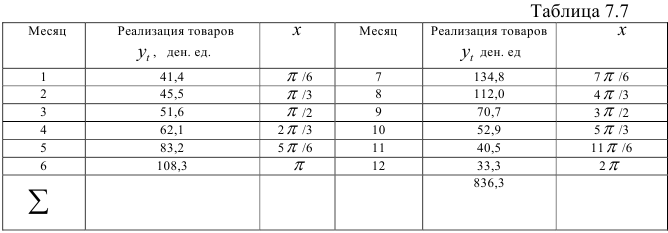
Наибольшее количество гармоник, которое можно рассчитать для этого ряда, равно 6. Вычислим коэффициенты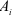 
и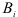 
:
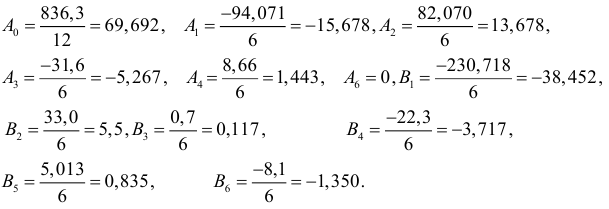
В целом модель сезонной волны имеет вид
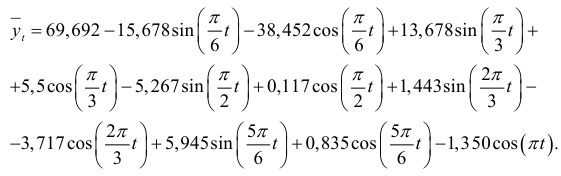
Дисперсии, учитываемые гармониками, составляют:
Теперь определим вклады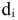 
шести гармоник в дисперсию динамического ряда по формуле:
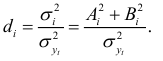
Так как общая дисперсия равна 1327,308, то часть общей дисперсии, учитываемая гармониками, составляет: первой — 64,97 %, второй — 8,22, третьей — 1,04, четвертой — 0,59, пятой — 1,36, шестой — 0,14 %.
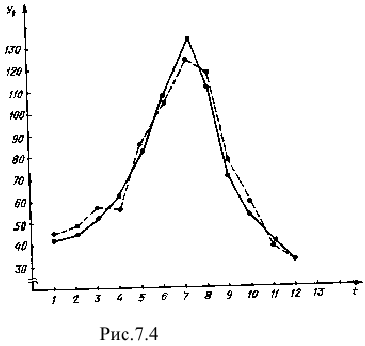
Как следует из данных, приведенных выше, шесть гармоник объясняют 76,32 % дисперсии динамического ряда. Наиболее важными являются первая и вторая гармоники, объясняющие 73,19 % общей дисперсии. В табл. 7.8 приведены значения, рассчитанные по функции (7.7), и модули относительных отклонений расчетных значений от фактических. Используя эти данные, вычисляем среднюю ошибку аппроксимации:
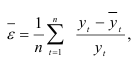
которая будет равна 0,0669, или 6,69 %.
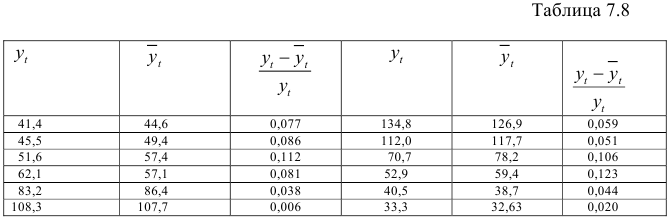
На рис. 7.4 отображены фактические данные (сплошная линия) и данные, сглаженные шестью гармониками (штриховая линия). Значения функции (7.7) достаточно близко расположены к фактическим данным.
Это подтверждается малым значением средней ошибки аппроксимации.
Изучение эволюции сезонной волны сезонных колебаний экономических явлений приведены ниже.
В заключение заметим, что после установления и выявления сезонной компоненты ее можно исключить из ряда динамики. Для этого исходные месячные или квартальные уровни динамического ряда делят на соответствующие сезонные индексы. После исключения сезонной компоненты уровни динамического ряда содержат тенденцию, циклическую и случайную компоненты.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
| Агрегатная модель компонент уровня ряда динамики |
| Выбор функции тренда |
| Анализ и моделирование случайной компоненты |
| Моделирование связных рядов динамики |
