Мультиколлинеарность экзогенных переменных
Методы устранения мультиколлинеарности:
Мультиколлинеарностью называется линейная зависимость между двумя или несколькими факторными признаками множественной линейной регрессии. Если факторные признаки связаны строгой линейной функциональной зависимостью, то мультиколлинеарность называется совершенной, а при существовании тесной корреляционной зависимости между факторными признаками -несовершенной. При существовании мультиколлинеарности могут возникнуть следующие последствия:
- Большие стандартные ошибки оценок параметров уравнения регрессии, что приводит к увеличению интервальных оценок, ухудшению их точности.
- Уменьшаются
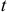 -статистики коэффициентов, что может привести к неоправданному выводу о значимости влияния соответствующего фактора на результативный признак.
-статистики коэффициентов, что может привести к неоправданному выводу о значимости влияния соответствующего фактора на результативный признак. - Становятся неустойчивыми оценки параметров уравнения регрессии при малейшем изменении данных.
- Затрудняется определение вклада каждого из факторных признаков в объясняемую уравнением регрессии дисперсию результативного признака.
- Возможно получение неверного знака у коэффициента регрессии.
Существует несколько признаков, по которым может быть установлена мультиколлинеорность.
- Коэффициент детерминации
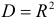 близок к единице, но некоторые из коэффициентов регрессии статистически незначимы, т. е. они имеют низкие
близок к единице, но некоторые из коэффициентов регрессии статистически незначимы, т. е. они имеют низкие 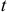 -статистики.
-статистики. - Между малозначимыми факторными признаками существует тесная корреляционная зависимость.
- Тесная частная корреляционная зависимость между факторными признаками.
Мультиколлинеарность может иметь место, если какой — либо факторный признак связан тесной корреляционной зависимостью с другими факторными признаками. Для выявления этой зависимости строятся уравнения регрессии каждого факторного признака 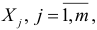 , на оставшиеся факторные признаки. Вычисляются соответствующие коэффициенты детерминации
, на оставшиеся факторные признаки. Вычисляются соответствующие коэффициенты детерминации 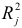 и оценивается их статистическая значимость на основе
и оценивается их статистическая значимость на основе 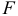 -статистики:
-статистики: 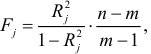 , где
, где 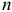 -число наблюдений,
-число наблюдений, 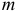 -число факторных признаков в первоначальном уравнении регрессии. Статистика
-число факторных признаков в первоначальном уравнении регрессии. Статистика 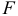 подчиняется распределению Фишера с числом степеней свободы
подчиняется распределению Фишера с числом степеней свободы 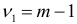 и
и 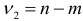 . Если коэффициент
. Если коэффициент 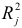 статистически значим, то есть основания считать, что между
статистически значим, то есть основания считать, что между 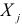 и другими факторными признаками существует корреляционная зависимость, следовательно, имеет место мультиколлинеарность. В противном случае, мультиколлинеарность отсутствует.
и другими факторными признаками существует корреляционная зависимость, следовательно, имеет место мультиколлинеарность. В противном случае, мультиколлинеарность отсутствует.
Прежде чем устранять мультиколлинеарность, определяется цель исследования. Если модель строится для прогнозирования, то при 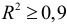 мультиколлинеарность не сказывается на прогнозных качествах модели. В других случаях, применяются методы для исключения мультиколлинеорности.
мультиколлинеарность не сказывается на прогнозных качествах модели. В других случаях, применяются методы для исключения мультиколлинеорности.
Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных.
Для уменьшения мультиколлинеарности увеличивается объем выборки, что приводит к увеличению статистической значимости коэффициентов регрессии.
Изменяется форма модели, или добавляются факторные признаки, не учтенные в модели, но существенно влияющие на результативный признак (зависимую переменную). Это приводит к уменьшению стандартных ошибок коэффициентов регрессии.
Выполняются преобразования уравнения регрессии, путем деления на один из факторных признаков и др.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

