Автокорреляция остатков регрессионной модели. Критерий Дарбина — Уотсона
Другой важной предпосылкой МНК является предположение о попарной независимости значений случайных отклонений (остатков) 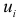 и
и 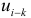 в вероятностном смысле, т.е.
в вероятностном смысле, т.е.
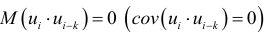
для
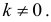
Корреляция между упорядоченными во времени или в пространстве последовательными или смещенными на лаг 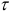 значениями одного и того же ряда наблюдений называется автокорреляцией.
значениями одного и того же ряда наблюдений называется автокорреляцией.
Автокорреляция остатков (отклонений) — это корреляция между последовательными значениями возмущающей переменной 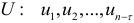 и
и 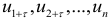 . Она обычно встречается в регрессионном анализе при изучении временных рядов. В экономических задачах значительно чаще встречается положительная автокорреляция
. Она обычно встречается в регрессионном анализе при изучении временных рядов. В экономических задачах значительно чаще встречается положительная автокорреляция
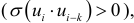
чем отрицательная автокорреляция
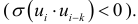
Положительная (отрицательная) автокорреляция вызывается постоянным направленным воздействием неучтенных в регрессионной модели факторами.
Последствия автокорреляции в определенной мере сходны с последствиями гетороскедастичности, т.е. все выводы, получаемые на основе соответствующих 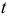 — и
— и 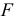 -статистик, определяющих значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели, поскольку оценки параметров уравнения регрессии, полученные с применением МНК, перестают быть эффективными.
-статистик, определяющих значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели, поскольку оценки параметров уравнения регрессии, полученные с применением МНК, перестают быть эффективными.
Для установления статистической независимости отклонений 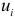 проверяется некоррелированность не любых, а только соседних величин
проверяется некоррелированность не любых, а только соседних величин 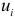 . Соседними значениями остатков
. Соседними значениями остатков 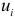 считаются соседние во времени или по возрастанию значений факторного признака
считаются соседние во времени или по возрастанию значений факторного признака 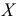 . Для анализа коррелированности этих величин коэффициент корреляции вычисляется по формуле:
. Для анализа коррелированности этих величин коэффициент корреляции вычисляется по формуле:
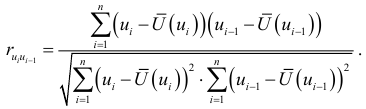
На практике, вместо коэффициента корреляции используют другие критерии. Наиболее распространенным критерием, позволяющим установить наличие автокорреляции остатков первого порядка, т.е. между соседними остаточными членами, является критерий Дарбина — Уотсона (см. п. 2.7).
При применении этого критерия формулируется основная гипотеза 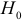 , состоящая в том, что автокорреляция остатков отсутствует:
, состоящая в том, что автокорреляция остатков отсутствует: 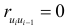 и альтернативная гипотеза
и альтернативная гипотеза 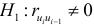 — автокорреляция остатков существует. Для проверки выдвинутой гипотезы
— автокорреляция остатков существует. Для проверки выдвинутой гипотезы 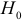 применяется статистика:
применяется статистика:
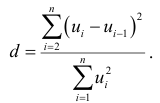
При больших значениях 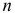 коэффициент корреляции и статистика
коэффициент корреляции и статистика 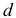 связаны равенством
связаны равенством
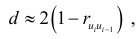
так как при больших значениях 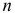 две суммы равны:
две суммы равны:
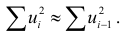
Из равенства (4.7) следует, что если 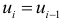 , то
, то 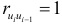 и
и 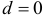 . Если
. Если 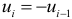 , то
, то 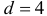 и
и 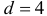 . Во всех других случаях
. Во всех других случаях 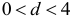 .
.
При случайном поведении отклонений (остатков) 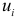 можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой — противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев
можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой — противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев 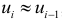 , а в другой
, а в другой 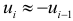 . Тогда
. Тогда
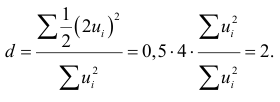
Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина -Уотсона. Следовательно, если 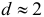 , то считаем отклонения от регрессии случайными (хотя в действительности они таковыми могут и не быть), а построенная эмпирическая линейная регрессия, вероятно, отражает реальную зависимость.
, то считаем отклонения от регрессии случайными (хотя в действительности они таковыми могут и не быть), а построенная эмпирическая линейная регрессия, вероятно, отражает реальную зависимость.
Для ответа на вопрос, какие значения статистики 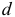 можно считать статистически близкими к двум, разработаны таблицы значений статистики Дарбина — Уотсона, позволяющие при данном числе наблюдений
можно считать статистически близкими к двум, разработаны таблицы значений статистики Дарбина — Уотсона, позволяющие при данном числе наблюдений 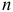 , количестве факторных признаков
, количестве факторных признаков 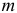 и заданном уровне значимости
и заданном уровне значимости 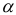 , определить границы области значений статистики
, определить границы области значений статистики 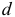 , при которых принимается или отклоняется гипотеза о наличии автокорреляции. Для заданных
, при которых принимается или отклоняется гипотеза о наличии автокорреляции. Для заданных 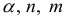 в таблице указываются два числа:
в таблице указываются два числа: 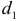 — нижняя граница и
— нижняя граница и 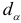 — верхняя граница. Выводы осуществляются по правилу:
— верхняя граница. Выводы осуществляются по правилу:
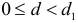 существует положительная автокорреляция остатков;
существует положительная автокорреляция остатков;
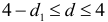 , существует отрицательная автокорреляция остатков;
, существует отрицательная автокорреляция остатков;
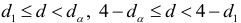 , вопрос о принятии или отвержении гипотезы о наличии автокорреляции остается открытым;
, вопрос о принятии или отвержении гипотезы о наличии автокорреляции остается открытым;
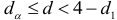 , автокорреляция отсутствует.
, автокорреляция отсутствует.
При грубой оценке считают, что если 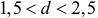 , то автокорреляция остатков отсутствует. Для более надежного вывода следует использовать таблицу. Отметим, что при наличии автокорреляции остатков построенное уравнение регрессии считается неудовлетворительным.
, то автокорреляция остатков отсутствует. Для более надежного вывода следует использовать таблицу. Отметим, что при наличии автокорреляции остатков построенное уравнение регрессии считается неудовлетворительным.
Применение статистики Дарбина — Уотсона основано на следующих предположениях:
- Регрессионные модели должны содержать свободный член.
- Случайные отклонения
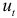 определяются по итерационной схеме
определяются по итерационной схеме 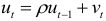 называемой авторегрессионной схемой первого порядка.
называемой авторегрессионной схемой первого порядка. - Эмпирические данные должны иметь одинаковую периодичность.
- Критерий не применяется для авторегрессионных моделей.
При подтверждении автокорреляции остатков в первую очередь необходимо проанализировать спецификацию модели, т. е. уточнить состав факторных признаков, оказывающих влияние на результативный признак. Если после этого автокорреляция имеет место, то применяются различные преобразования модели, устраняющие автокорреляцию.
Для устранения автокорреляции можно воспользоваться авторегрессионной схемой первого порядка AR(1), применение которой рассмотрим на парной линейной регрессии
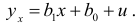
Тогда наблюдения 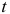 и
и 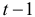 удовлетворяют таким же уравнениям:
удовлетворяют таким же уравнениям:
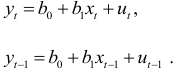
Предположим, что случайные отклонения описываются авторегрессионной моделью первого порядка:
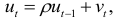
где 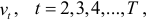 , — случайные отклонения, удовлетворяющие всем предпосылкам МНК,
, — случайные отклонения, удовлетворяющие всем предпосылкам МНК, 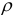 — коэффициент автокорреляции. Умножим соотношение (4.10) на
— коэффициент автокорреляции. Умножим соотношение (4.10) на 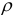 и вычтем из (4.9):
и вычтем из (4.9):
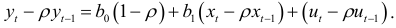
Введем обозначения
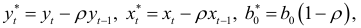
и учитывая (4.11), получим уравнение регрессии в виде:
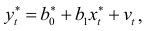
коэффициенты 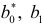 которого можно вычислить, применяя МНК. Коэффициенты
которого можно вычислить, применяя МНК. Коэффициенты 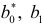 будут наилучшими оценками параметров уравнения регрессии изучаемой зависимости, так как случайные отклонения
будут наилучшими оценками параметров уравнения регрессии изучаемой зависимости, так как случайные отклонения 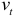 удовлетворяют предпосылкам МНК. При этом способе устранения автокорреляции происходит потеря первого наблюдения, что может привести к потере эффективности при малом числе наблюдений. Эта проблема обычно преодолевается с помощью поправки Прайса — Винстена:
удовлетворяют предпосылкам МНК. При этом способе устранения автокорреляции происходит потеря первого наблюдения, что может привести к потере эффективности при малом числе наблюдений. Эта проблема обычно преодолевается с помощью поправки Прайса — Винстена:
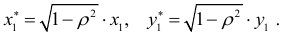
Если значение коэффициента автокорреляции 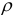 неизвестно, то в качестве его оценки можно взять коэффициент корреляции
неизвестно, то в качестве его оценки можно взять коэффициент корреляции 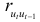 , вычисленный по формуле
, вычисленный по формуле 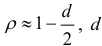 — статистика Дарбина — Уотсона. Существуют и другие методы оценивания
— статистика Дарбина — Уотсона. Существуют и другие методы оценивания 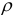 : методы Кохрана — Оркатта, Хилдретта — Лy.
: методы Кохрана — Оркатта, Хилдретта — Лy.
В случае, когда автокорреляция остатков велика, то применяется метод первых разностей. При этом методе уравнение регрессии (4.12), в котором полагаем 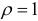 , преобразуется к виду:
, преобразуется к виду:
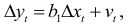
где
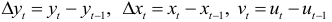
коэффициент 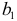 оценивается по МНК.
оценивается по МНК.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

