Методы смягчения проблемы гетероскедастичности
При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения этого недостатка. Вид преобразований зависит от того, известны или неизвестны дисперсии 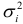 отклонений
отклонений 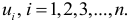 .
.
А). Если для каждого наблюдения известны значения 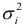 , то устранить гетероскедастичность можно, разделив каждое эмпирическое значение на соответствующее ему значение дисперсии и для преобразованных эмпирических данных можно применить метод наименьших квадратов при построении регрессии.
, то устранить гетероскедастичность можно, разделив каждое эмпирическое значение на соответствующее ему значение дисперсии и для преобразованных эмпирических данных можно применить метод наименьших квадратов при построении регрессии.
Рассмотрим парную линейную регрессию
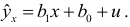
Разделим все члены уравнения на
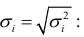
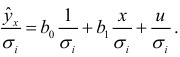
Обозначив
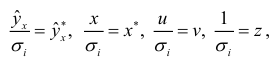
уравнение регрессии
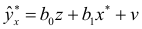
без свободного члена, но с дополнительным факторным признаком 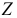 и с преобразованным отклонением
и с преобразованным отклонением 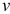 , для которого выполняется условие гомоскедастичноти. Действительно,
, для которого выполняется условие гомоскедастичноти. Действительно,
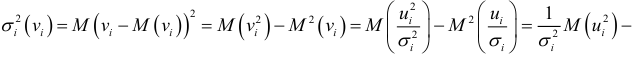
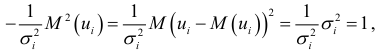
так как
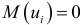
согласно первой предпосылке.
Рассмотренный метод преобразований называется взвешенным методом наименьших квадратов (ВМНК), который включает следующие шаги.
- Значения каждой пары эмпирических данных
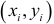 делят на известную величину
делят на известную величину 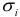 . Тем самым наблюдениям с наименьшими дисперсиями придаются большие «веса», чем наблюдениям с большими дисперсиями. При этом увеличивается вероятность получения более точных оценок.
. Тем самым наблюдениям с наименьшими дисперсиями придаются большие «веса», чем наблюдениям с большими дисперсиями. При этом увеличивается вероятность получения более точных оценок. - Для преобразования значений
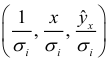 строится регрессии при помощи метода наименьших квадратов.
строится регрессии при помощи метода наименьших квадратов.
Б). Если фактические значения дисперсий 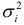 отклонений неизвестны, то формулируются различные предположения о дисперсиях:
отклонений неизвестны, то формулируются различные предположения о дисперсиях:
- дисперсии
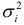 пропорциональны
пропорциональны 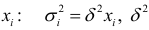 — коэффициент пропорциональности. Тогда все члены уравнения (4.2) делим на
— коэффициент пропорциональности. Тогда все члены уравнения (4.2) делим на 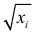 :
:
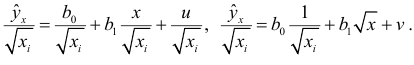
Можно показать, что для случайных отклонений 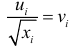 выполняется условие гомоскедастичности, Следовательно, для построения уравнения регрессии (4.3) можно применить МНК. Оценив коэффициенты
выполняется условие гомоскедастичности, Следовательно, для построения уравнения регрессии (4.3) можно применить МНК. Оценив коэффициенты 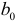 и
и 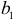 возвращаемся к исходному уравнению регрессии (4.2).
возвращаемся к исходному уравнению регрессии (4.2).
- дисперсии
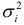 пропорциональны
пропорциональны 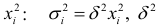 -коэффициент пропорциональности. Соответствующим преобразованием будет деление всех членов уравнения (4.2) на
-коэффициент пропорциональности. Соответствующим преобразованием будет деление всех членов уравнения (4.2) на 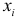 :
:
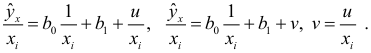
После определения оценок параметров 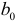 и
и 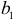 , применяя МНК, возвращаемся к исходному уравнению регрессии (4.2).
, применяя МНК, возвращаемся к исходному уравнению регрессии (4.2).
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

