Измерение интенсивности линейной корреляционной связи
Мы рассмотрели, как определяется форма связи между факторным и результативным признаками. Изучим теперь показатели интенсивности этой связи.
При прямолинейной связи общим показателем интенсивности является линейный коэффициент корреляции (просто коэффициент корреляции)
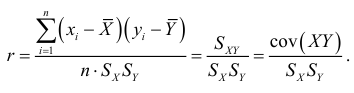
Коэффициент корреляции является безразмерной величиной, так как сравниваются не индивидуальные отклонения, а нормированные отклонения
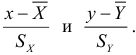
Среднее произведение нормированных отклонении и дает коэффициент корреляции. Коэффициент корреляции удовлетворяет свойствам:
• Величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин 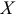 и
и 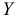 ;
;
• Коэффициент корреляции не превосходит по абсолютной величине единицы, т.е. 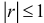 ;
;
• Коэффициент корреляции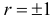 тогда и только тогда, когда между случайными величинами
тогда и только тогда, когда между случайными величинами 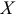 и
и 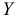 существует линейная функциональная зависимость;
существует линейная функциональная зависимость;
• Если между случайными величинами 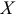 и
и 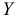 отсутствует хотя бы одна из корреляционных связей, то коэффициент корреляции равен нулю;
отсутствует хотя бы одна из корреляционных связей, то коэффициент корреляции равен нулю;
• Условие 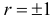 является необходимым и достаточным условием для совпадения регрессий
является необходимым и достаточным условием для совпадения регрессий 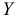 на
на 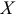 и
и 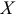 на
на 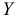 .
.
Степень интенсивности корреляционной связи можно определить из табл. 1.1.

Отметим, что коэффициент корреляции не отражает направление зависимости, т.е. он является функцией, симметричной относительно 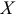 и
и 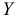 .
.
Средняя квадратичная ошибка коэффициента корреляции определяется по формуле
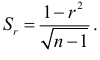
Наряду с коэффициентом корреляции и корреляционным отношением в эконометрике применяется коэффициент детерминации, отражающий, в какой мере функция регрессии определяется факторными признаками, содержащимися в ней.
Для определения коэффициента детерминации дисперсию, характеризующую рассеяние наблюдаемых значений переменной 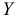 около ее среднего, разложим на две составляющие:
около ее среднего, разложим на две составляющие:
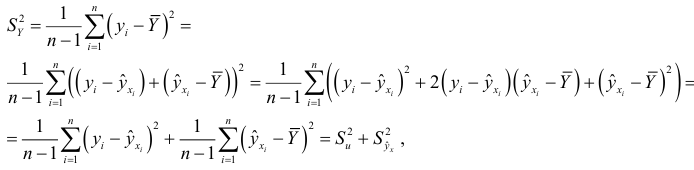
где
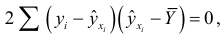
так как прямая регрессии проходит через среднюю точку 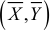 корреляционного поля.
корреляционного поля.
Дисперсия 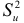 представляет собой ту часть общей дисперсии
представляет собой ту часть общей дисперсии 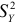 , которая обусловлена случайностью и изменчивостью прочих неучтенных факторов и не объясняется функцией регрессии. Из равенства
, которая обусловлена случайностью и изменчивостью прочих неучтенных факторов и не объясняется функцией регрессии. Из равенства
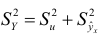
видно, что чем меньше 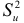 , тем меньше эмпирические значения
, тем меньше эмпирические значения 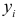 отклоняются от значений регрессии
отклоняются от значений регрессии 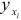 . Вторая составляющая общей дисперсии
. Вторая составляющая общей дисперсии 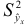 является дисперсией значений регрессии
является дисперсией значений регрессии 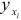 . Рассеяние значений регрессии определяется значением коэффициента регрессии, следовательно, дисперсия
. Рассеяние значений регрессии определяется значением коэффициента регрессии, следовательно, дисперсия 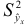 обусловлена влиянием факторного признака. Поэтому чем больше
обусловлена влиянием факторного признака. Поэтому чем больше 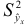 . по сравнению с
. по сравнению с 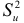 , тем больше общая дисперсия формируется за счет влияния факторного признака и, следовательно, связь между двумя переменными
, тем больше общая дисперсия формируется за счет влияния факторного признака и, следовательно, связь между двумя переменными 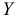 и
и 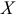 более интенсивная. Тогда в качестве показателя интенсивности связи (или оценки доли влияния переменной
более интенсивная. Тогда в качестве показателя интенсивности связи (или оценки доли влияния переменной 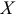 на
на 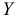 ) используется отношение
) используется отношение
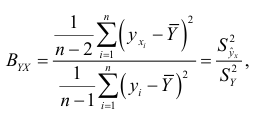
которое указывает, какая часть общего рассеяния значений 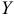 обусловлена изменчивостью переменной
обусловлена изменчивостью переменной 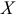 , и называется коэффициентом детерминации. Чем большую долю в общей дисперсии составляет
, и называется коэффициентом детерминации. Чем большую долю в общей дисперсии составляет 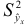 , тем лучше выбранная функция регрессии соответствует эмпирическим данным.
, тем лучше выбранная функция регрессии соответствует эмпирическим данным.
Коэффициент детерминации 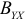 изменяется в пределах от 0 до 1
изменяется в пределах от 0 до 1 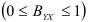 . Если
. Если 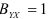 , то все эмпирические значения
, то все эмпирические значения 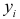 лежат на регрессионной прямой, т.е.
лежат на регрессионной прямой, т.е.
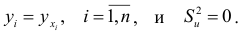
Следовательно, переменные 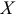 и
и 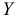 связаны линейной функциональной зависимостью. Если
связаны линейной функциональной зависимостью. Если
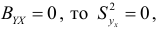
а «остаточная» дисперсия 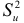 равна общей дисперсии
равна общей дисперсии 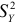 т.е.
т.е. 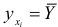 . В этом случае линия регрессии параллельна оси абсцисс и, следовательно, ни о какой статистической линейной зависимости не может быть речи.
. В этом случае линия регрессии параллельна оси абсцисс и, следовательно, ни о какой статистической линейной зависимости не может быть речи.
Таким образом, чем больше коэффициент детерминации 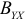 приближается к единице, тем лучше определена регрессия.
приближается к единице, тем лучше определена регрессия.
Коэффициент детерминации 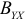 — величина безразмерная. Он не зависит от единиц измерения признаков
— величина безразмерная. Он не зависит от единиц измерения признаков 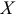 и
и 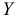 и не изменяется при преобразовании переменных. Подставляя выражения
и не изменяется при преобразовании переменных. Подставляя выражения
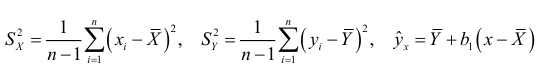
в формуле
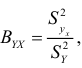
получаем:
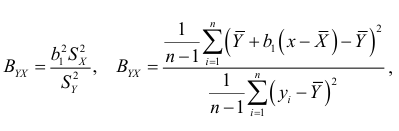
откуда, так как
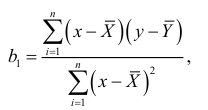
выводим формулу коэффициента детерминации, удобную для вычисления:
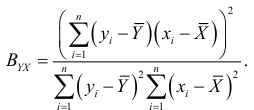
Укажем соотношения между коэффициентами корреляции, регрессии и детерминации при однофакторной линейной регрессии:
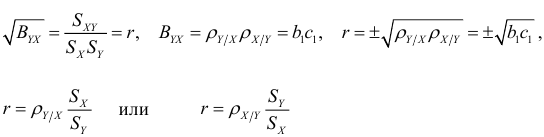
(перед корнем ставится знак коэффициента регрессии).
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

