Построение регрессионной прямой методом наименьших квадратов
Если, исходя из профессионально-теоретических соображений в сочетании с исследованием расположения точек на корреляционном поле или других соображений, предполагают линейный характер зависимости усредненных значений результативного признака, то эту зависимость выражают с помощью функции линейной регрессии. Эта функция, называемая эмпирической регрессией, служит оценкой линейной функциональной связи между результативным и факторным признаками.
На результативный признак оказывает влияние и ряд других факторов. Чтобы элиминировать (сгладить) влияние этих факторов, нужно произвести выравнивание фактических величин 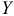 на основании предположения, что между
на основании предположения, что между 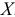 и
и 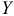 существует функциональная зависимость вида:
существует функциональная зависимость вида:
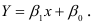
При этом фактические значения 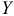 заменяются значениями, вычисленными па формуле
заменяются значениями, вычисленными па формуле
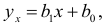
где 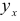 — оценка условного математического ожидания
— оценка условного математического ожидания 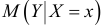 ,
, 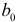 и
и 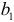 — оценки неизвестных параметров
— оценки неизвестных параметров 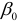 и
и 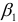 называемые эмпирическими коэффициентами регрессии. В конкретном случае
называемые эмпирическими коэффициентами регрессии. В конкретном случае
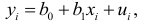
где отклонение 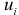 — оценка теоретического отклонения. Оценки
— оценка теоретического отклонения. Оценки 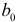 и
и 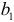 практически всегда отличаются от истинных значений коэффициентов
практически всегда отличаются от истинных значений коэффициентов 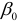 и
и 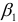 что приводит к несовпадению эмпирической и теоретической линий регрессий.
что приводит к несовпадению эмпирической и теоретической линий регрессий.
Так как все факторы, кроме фактора 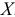 , рассматриваются как постоянные средние величины и выражены параметрами
, рассматриваются как постоянные средние величины и выражены параметрами 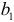 и
и 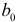 , то и сглаженные величины
, то и сглаженные величины 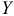 представляют собой средние
представляют собой средние 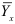 . Неизвестные параметры
. Неизвестные параметры 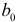 и
и 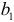 входящие в уравнение (1.1), определяются методом наименьших квадратов:
входящие в уравнение (1.1), определяются методом наименьших квадратов:
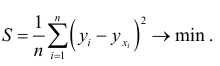
Величина 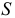 является функцией параметров
является функцией параметров 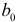 и
и 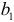 . Тогда, в силу необходимого условия экстремума, частные производные
. Тогда, в силу необходимого условия экстремума, частные производные 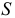 по
по 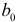 и
и 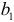 , должны быть равны нулю:
, должны быть равны нулю:
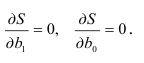
Выполнив преобразования и решив систему нормальных уравнений:
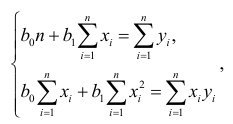
получим:
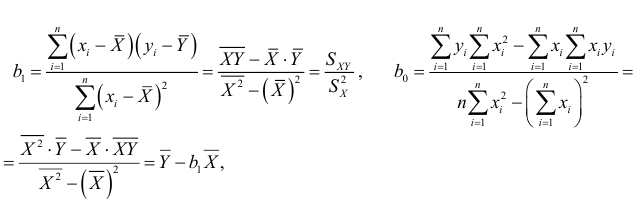
где
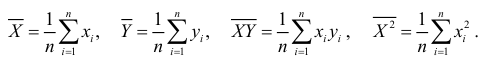
Оценки MHK являются: а) функциями от выборки (эмпирических данных); б) точечными оценками теоретических коэффициентов регрессии.
Эмпирическая прямая регрессии проходит через точку 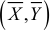 и среднее значений отклонений равно нулю
и среднее значений отклонений равно нулю 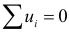 . Случайные отклонения
. Случайные отклонения 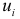 не коррелированны с наблюдаемыми значениями
не коррелированны с наблюдаемыми значениями 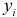 зависимой переменной
зависимой переменной 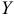 .
.
Параметр 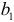 называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси
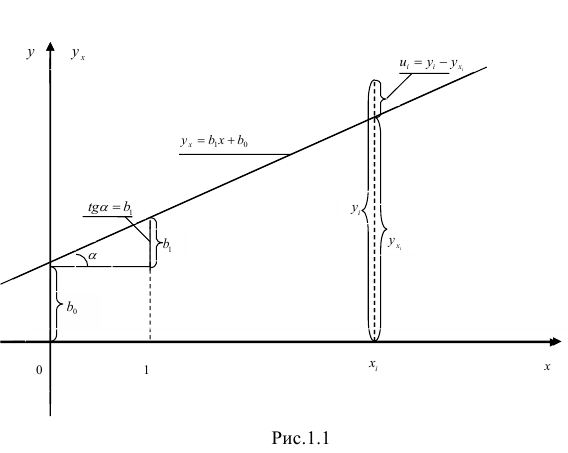
называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси 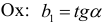 (рис. 1.1).
(рис. 1.1).
Коэффициент регрессии является мерой зависимости переменной 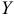 от переменной
от переменной 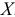 , т.е.
, т.е. 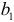 указывает, как в среднем изменяется значение переменной
указывает, как в среднем изменяется значение переменной 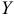 при изменении переменной
при изменении переменной 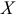 на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.
на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.
Отыскание значений коэффициента регрессии представляет большей практический интерес, если ставится вопрос о прогнозе изменений какого-либо показателя в связи с изменением того или иного условия. В частности, коэффициент регрессии используется для определения эластичности спроса и потребления.
В общем случае коэффициент эластичности представляет собой процентное изменение результативного признака при изменении факторного признака на один процент. Он вычисляется по формуле
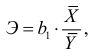
где 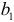 — коэффициент регрессии;
— коэффициент регрессии; 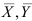 — средние значения соответственно факторного и результативного признаков.
— средние значения соответственно факторного и результативного признаков.
Например, коэффициент эластичности потребления выражает процентное изменение потребления или спроса на данный товар при изменении известных условий (дохода, цены и т.д.) на один процент.
Параметры 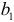 и
и 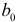 прямой регрессии — не безразмерные величины.
прямой регрессии — не безразмерные величины.
Постоянная регрессии 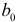 имеет размерность признака
имеет размерность признака 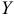 . Размерность коэффициента регрессии
. Размерность коэффициента регрессии 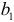 представляет собой отношение размерности результативного признака к размерности факторного признака.
представляет собой отношение размерности результативного признака к размерности факторного признака.
После вычисления оценок параметров регрессии 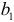 и
и 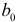 , а также средних значений
, а также средних значений 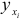 по формуле
по формуле 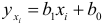 вычисляем остатки
вычисляем остатки
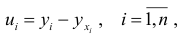
которые используются в качестве характеристики точности оценки регрессии или степени согласованности расчетных значений регрессии и наблюдаемых значений переменной 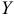 . Для характеристики меры разброса фактических данных
. Для характеристики меры разброса фактических данных 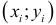 вокруг значений регрессии вычисляют дисперсию остатков:
вокруг значений регрессии вычисляют дисперсию остатков:
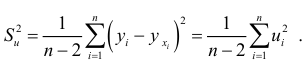
Геометрический смысл параметров прямой регрессии следует из рис. 1.1.
Используя дисперсию остатков, можно указать среднюю квадратичную ошибку коэффициента регрессии:
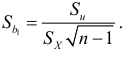
Кроме уравнения регрессии 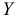 на
на 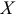 для тех же эмпирических данных может быть найдено уравнение регрессии
для тех же эмпирических данных может быть найдено уравнение регрессии 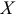 на
на 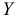 :
:
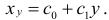
Коэффициенты 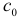 и
и 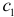 находятся по аналогичным формулам:
находятся по аналогичным формулам:
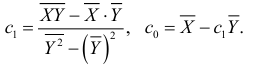
Как уже отмечалось, функция регрессии указывает, в какой степени изменяются значения результативного признака в соответствии с изменением факторного признака. Однако этого недостаточно для глубокого изучения их взаимосвязи. Нужно измерить еще интенсивность между изучаемыми факторами. Оценки, полученные с помощью уравнения регрессии, имеют точность тем большую, чем интенсивнее корреляция.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

