Пример №30.
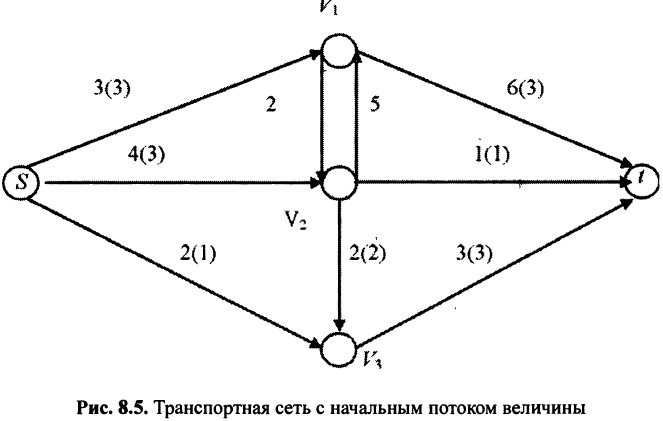
Найдем максимальный поток в сети, показанной на рис. 8.2. Для уменьшения количества итераций начнем с ненулевого допустимого потока (рис. 8.5).
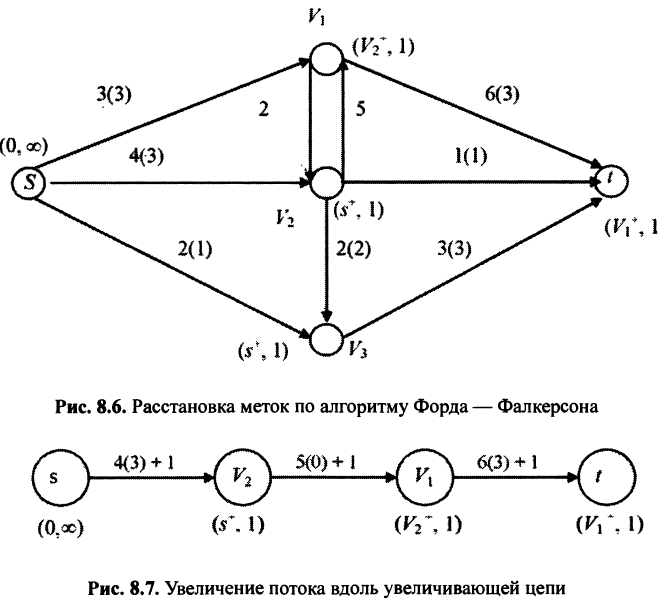
Шаг 1. Метим источник меткой 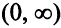 . Шаг 2. Из вершины
. Шаг 2. Из вершины 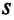 можно пометить вершину
можно пометить вершину 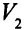 меткой
меткой 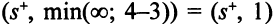 и вершину
и вершину 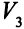 меткой
меткой 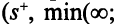
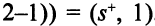 . Из вершины
. Из вершины 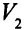 помечается вершина
помечается вершина 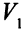 меткой
меткой 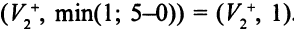 . Из вершины
. Из вершины 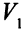 метится вершина
метится вершина 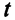 меткой
меткой 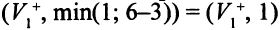 (рис. 8.6).
(рис. 8.6).
Шаг 3. Найдена увеличивающая цепь. Вершина 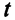 помечена от вершины
помечена от вершины 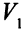 , вершина
, вершина 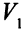 — от вершины
— от вершины 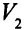 , а вершина
, а вершина 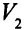 — от вершины
— от вершины 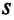 . Причем все вершины помечены по прямым дугам.
. Причем все вершины помечены по прямым дугам.
Шаг 4. Увеличивающая цепь имеет вид 
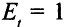 . На каждой дуге увеличивающей цепи величина потока возрастает на 1 (рис. 8.7).
. На каждой дуге увеличивающей цепи величина потока возрастает на 1 (рис. 8.7).
Шаг 5. Стираем все пометки и возвращаемся к шагу 1 (рис. 8.8).
Шаг 2. От вершины 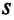 можно пометить вершину
можно пометить вершину 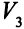 меткой
меткой 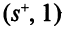 . От вершины
. От вершины 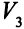 по обратной дуге можно пометить вершину
по обратной дуге можно пометить вершину 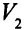 меткой
меткой 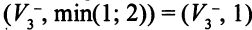 . От вершины
. От вершины 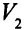 по прямой дуге метится вершина
по прямой дуге метится вершина 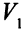 меткой
меткой 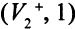 , а от вершины
, а от вершины 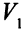 метится сток — меткой
метится сток — меткой 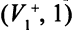 (рис. 8.8).
(рис. 8.8).
Шаг 3. Вершина 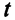 получила пометку, следовательно, поток в сети можно увеличить.
получила пометку, следовательно, поток в сети можно увеличить.
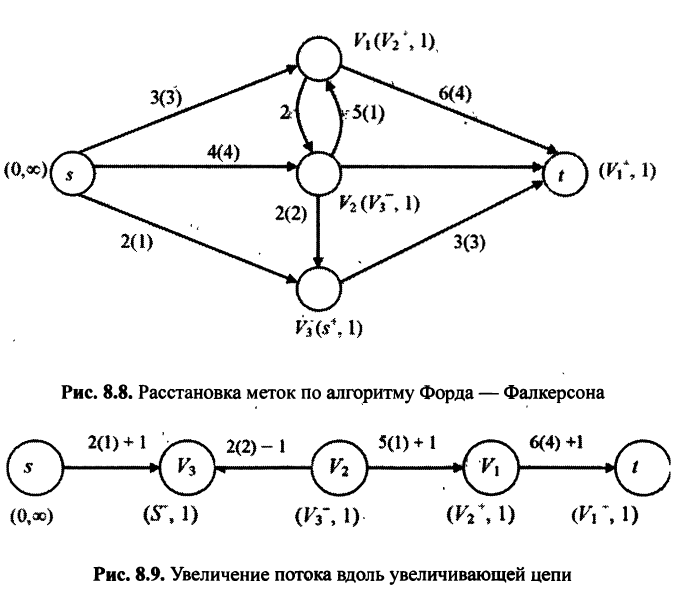
Шаг 4. Увеличивающая цепь имеет вид
По ней можно увеличить поток на 1 (рис. 8.9).
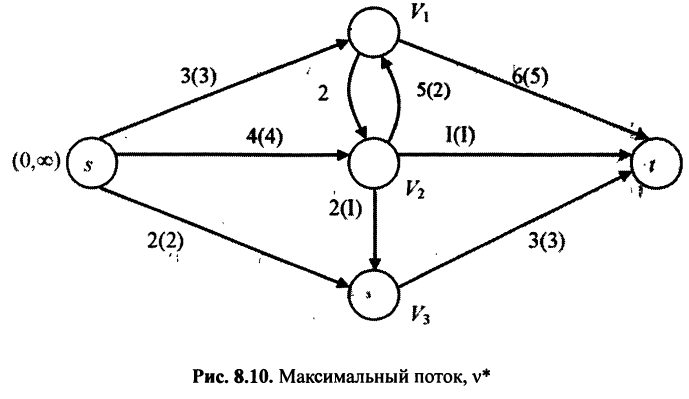
Шаг 5. Стираем все пометки и возвращаемся к шагу 1 (рис. 8.10).
Шаг 2. Все дуги, выходящие из источника, насыщены. Ни одной из вершин нельзя приписать метку. Следовательно, найден максимальный поток. Множество  помеченных вершин содержит единственную вершину
помеченных вершин содержит единственную вершину 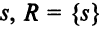 . Тогда
. Тогда
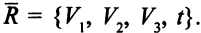
Минимальный разрез 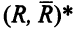 составляют дуги
составляют дуги
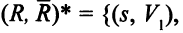
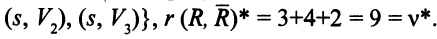
Конец.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №28. Построить увеличивающую цепь для паросочетания |
| Пример №29. Решим ЗН с матрицей затрат, заданной в табл. 7.4. |
| Пример №1. Задача распределения ресурсов. |
| Пример №2. Задача о раскрое. |

