Пример №1. Задача распределения ресурсов.
Предприятие изготовляет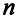 
типов продукции, для производства которой требуется 
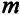видов сырья. Для изготовления единицы 
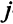-го типа продукции требуется 
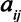единиц сырья 
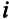-го вида, 
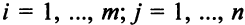(некоторые из чисел 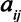могут равняться нулю). Запасы сырья ограничены и составляют 
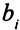единиц для 1-го вида сырья, 
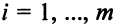. Прибыль от реализации одной единицы продукции 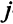-го типа равна 
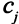единиц, 
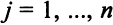. Сколько единиц продукции каждого вида нужно произвести, чтобы получить максимальную прибыль и уложиться в имеющиеся запасы ресурсов?
Описывая математическую модель задачи линейного программирования, будем последовательно определять неизвестные задачи, целевую функцию и систему ограничений.
Описание неизвестных Неизвестно, сколько единиц продукции каждого типа нужно произвести. Обозначим эти величины через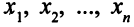 
. Всего в задаче 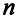неизвестных, 
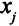— количество единиц продукции 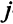-го типа, .
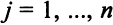Описание целевой функции. Требуется максимизировать прибыль от реализации продукции. Если единица продукции первого типа приносит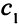 
единиц прибыли, то прибыль от реализации 
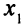единиц этой продукции составит 
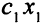единиц прибыли.
Соответственно,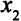 
единиц продукции второго типа дадут 
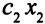единиц прибыли. Тогда прибыль от реализации всей продукции равна
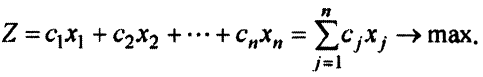
Описание системы ограничений. Запасы сырья ограничены. Подсчитаем, сколько сырья первого вида уйдет на производство всей продукции. Если на производство единицы продукции первого типа требуется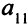 
единиц сырья первого вида, то на производство 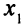единиц этой продукции будет затрачено 
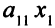единиц сырья первого вида. Для выпуска 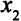единиц продукции второго типа потребуется 
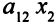единиц сырья первого вида. Чтобы произвести 
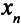единиц продукции 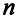-го типа, нужно затратить 
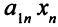единиц сырья первого вида. Всего же потребуется
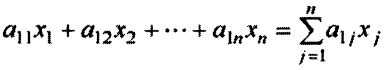
единиц сырья первого вида. Расход этого вида сырья не может превысить имеющегося запаса, должно выполняться неравенство
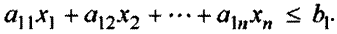
Подобным образом составляются ограничения по запасам сырья остальных видов. Система ограничений такова:
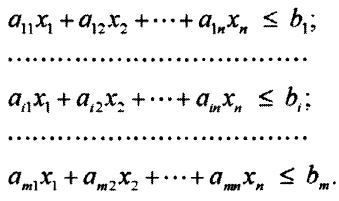
Всего в системе 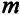ограничений по запасам. Кроме того, необходимо добавить еще условие неотрицательности переменных; нельзя выпускать отрицательное число единиц продукции:
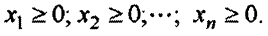
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №29. Решим ЗН с матрицей затрат, заданной в табл. 7.4. |
| Пример №30. Найдем максимальный поток в сети, показанной на рис. 8.2. |
| Пример №2. Задача о раскрое. |
| Пример №3. Задача о смеси. |
