Задача 4.9.
К началу текущей пятилетки на предприятии установлено новое оборудование. Зависимость производительности этого оборудования от времени его использования предприятием, а также зависимость затрат на содержание и ремонт оборудования при различном времени его использования приведены в табл. 4.1.
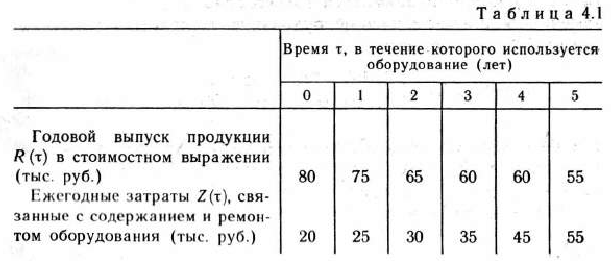
Зная, что затраты, связанные с приобретением н установкой нового оборудования, идентичного с установленным, составляют 40 тыс. руб., а заменяемое оборудование списывается, составить такой план замены оборудования в течение пятилетки, при котором общая прибыль за данный период времени максимальна.
Решение:
Эту задачу можно рассматривать как задачу динамического программирования, в которой в качестве системы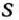 
выступает оборудование. Состояния этой системы определяются фактическим временем использования оборудования (его возрастом) 
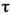, т. е. описываются единственным параметром .
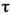В качестве управлений выступают решения о замене и сохранении оборудования, принимаемые в начале каждого года. Обозначим через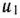 
решение о сохранении оборудования, а через 
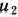—решение о замене оборудования. Тогда задача состоит в нахождении такой стратегии управления, определяемой решениями, принимаемыми к началу каждого года, при которой общая прибыль предприятия за пятилетку является максимальной.
Таким образом, мы сформулировали исходную задачу в терминах задачи динамического программирования. Эта задача обладает свойствами аддитивности и отсутствия последействия. Следовательно, ее решение можно найти с помощью описанного выше алгоритма решения задачи динамического программирования, реализуемого в два этапа. На первом этапе при движении от начала 5-го года пятилетки к началу 1-го года для каждого допустимого состояния оборудования найдем условное оптимальное управление (решение), а на втором этапе при движении от начала 1-го года пятилетки к началу 5-го года из условных оптимальных решений для каждого года составим оптимальный план замены оборудования на пятилетку.
Для определения условных оптимальных решений сначала необходимо составить функциональное уравнение Беллмана.
Так как мы предположили, что к началу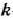 
-го года 
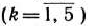может приниматься только одно из двух решений — заменять или не заменять оборудование, то прибыль предприятия за 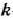-й год составит
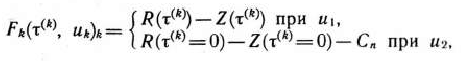
где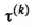 
—возраст оборудования к началу 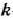-го года 
; 
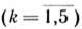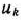— управление, реализуемое к началу 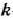-го года; 
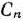— стоимость нового оборудования.
Таким образом, в данном случае уравнение Беллмана имеет вид
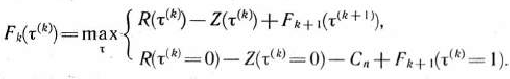
Используя теперь уравнение (9), приступаем к нахождению решения исходной задачи. Это решение начинаем с определения условно оптимального управления (решения) для последнего (5-го) года пятилетки, в связи с чем находим множество допустимых состояний оборудования к началу данного года пятилетки. Так как к началу пятилетки имеется новое оборудование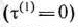 
, то возраст оборудования к началу 5-го года может составлять I, 2, 3 и 4 года. Поэтому допустимые состояния системы на данный период времени таковы:
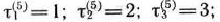
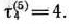
Для каждого из этих состояний найдем условно оптимальное решение и соответствующее значение функции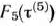 
. Используя уравнение (9) и соотношение 
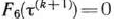(так как рассматривается последний год расчетного периода), получаем
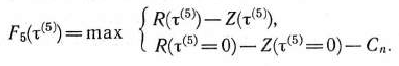
Подставляя теперь в формулу (10) вместо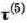 
его значение, равное 1, и учитывая данные табл. 4.1, находим
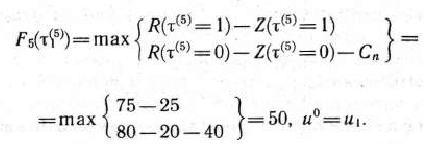
Значит, условно оптимальное решение в данном случае есть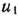 
.
Проведем аналогичные вычисления для других допустимых состояний оборудования к началу 5-го года пятилетки:
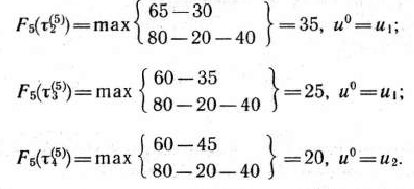
Полученные результаты вычислений сводим в табл.
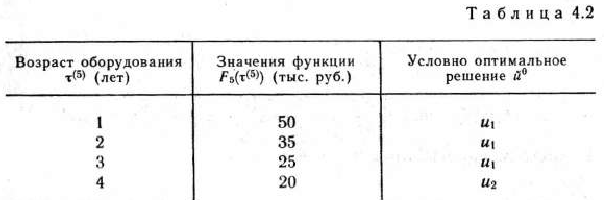
Рассмотрим теперь возможные состояния оборудования к началу 4-года пятилетки. Очевидно, допустимыми состояниями являются
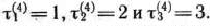
Для каждого из них определяем условно оптимальное решение и соответствующее значение функции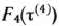 
. Для этого используем уравнение (9) и данные табл. 4.1 и 4.2. Так, в частности, для 
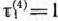имеем
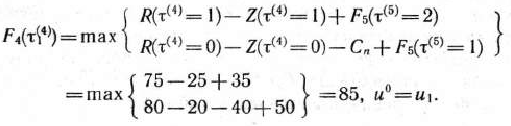
Аналогично находим
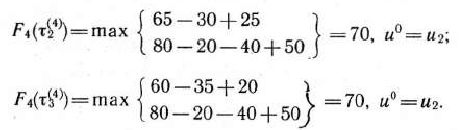
Полученные результаты вычислений записываем в табл. 4.3.
Определим теперь условно оптимальное решение для каждого из допустимых состояний оборудования к началу 3-го года пятилетки. Очевидно, такими состояниями являются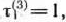 
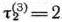. В соответствии с уравнением (9) имеем
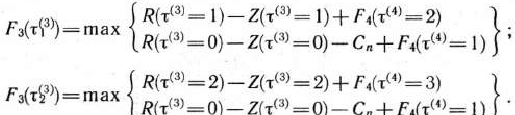
Используя данные табл. 4.1 и 4,3, получаем
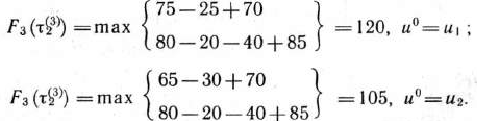
Из последнего выражения видно, что если к началу 3-го года пятилетки возраст оборудования составляет два года, то независимо от того, будет ли принято решение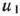 
или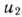 
, величина прибыли окажется одной и той же. Это означает, что в качестве условно оптимального решения можно взять любое, например 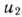. Полученные значения для 
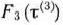и соответствующие условно оптимальные решения записываем в табл. 4.4.
Наконец, рассмотрим допустимые состояния оборудования к началу 2-го года пятилетки. Очевидно, на данный момент времени возраст оборудования может быть равен только лишь одному году. Поэтому предстоит сравнить лишь два возможных решения: сохранить оборудование или произвести замену. Анализ такого сравнения характеризуется данными табл. 4.5.
Согласно условию, к началу пятилетки установлено новое оборудование. Поэтому проблемы выбора между сохранением и заменой оборудования не существует: оборудование следует сохранить. Значит, условно оптимальным решением является 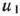, а значение функции
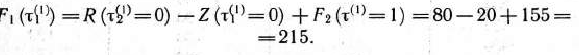
Таким образом, максимальная прибыль предприятия может быть равной 215тыс. руб. Она соответствует оптимальному плану замены оборудования, который получается на основе данных табл. 4.5, 4.4, 4.3 и 4.2, т. е. в результате реализации второго этапа вычислительного процесса, состоящего в прохождении всех рассмотренных шагов с начала 1-го до начала 5-го года пятилетки. Для 1-го года пятилетки решение единственно — следует сохранить оборудование. Значит, возраст оборудования к началу 2-го года пятилетки равен одному году. Тогда в соответствии с данными табл. 4.5 оптимальным решением для 2-го года пятилетки является решение о сохранении оборудования. Реализация такого решения приводит к тому, что возраст оборудования к началу 3-го года пятилетки становится равным двум годам. При таком возрасте (см. табл. 4.4) оборудование в 3-м году пятилетки следует заменить. После замены оборудования его возраст к началу 4-го года пятилетки составит один год. Как видно из табл. 4.3, при таком возрасте оборудования его менять не следует. Поэтому возраст оборудования к началу 5-го года пятилетки составит два года, т. е. менять оборудование нецелесообразно (табл. 4.2).
Итак, получается следующий оптимальный план замены оборудования (табл. 4.6).
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
