Задача 3.22.
Найти максимальное значение функции
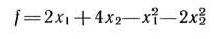
при условиях
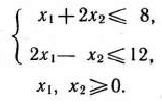
Решение:
Функция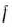 
является вогнутой, так как представляет собой сумму линейной функции
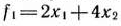
(которую можно рассматривать как вогнутую) и квадратичной формы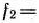 
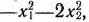, которая является отрицательно-определенной и, следовательно, также вогнутой. Система ограничений задачи включает только лишь линейные неравенства. Следовательно, можно воспользоваться теоремой Куна—Таккера. Составим функцию Лагранжа
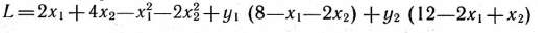
и запишем в виде выражений (39) —(43) необходимые и достаточные условия существования седловой точки построенной функции:
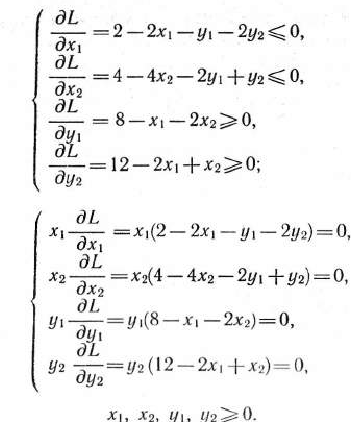
Систему линейных неравенств (47) перепишем следующим образом:
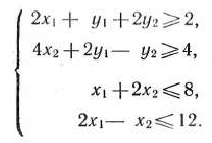
Вводя теперь дополнительные неотрицательные переменные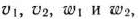 
обращающие неравенства (47) в равенства, получим
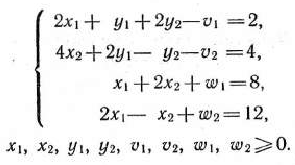
Учитывая равенства (51), можно записать:
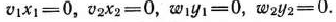
Если теперь найти базисное решение системы линейных уравнений (51) с учетом выполнения равенств (53), то будет получена седловая точка функции Лагранжа для исходной задачи, т. е. определено оптимальное решение.
Для нахождения базисного решения системы линейных уравнений (51) воспользуемся методом искусственного базиса. В первое и второе уравнения системы (51) соответственно добавим дополнительную неотрицательную переменную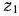 
и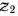 
и рассмотрим задачу линейного программирования, состоящую в определении максимального значения функции
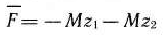
при условиях
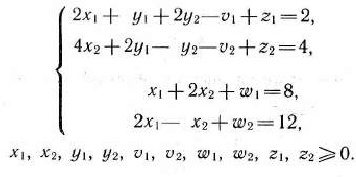
В результате решения задачи (54) —(56) [отметим, что при этом решении учитываются условия (53) | находим допустимое базисное решение системы линейных уравнений (55) (табл. 3.1):
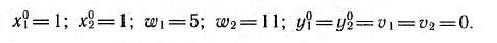
Так как
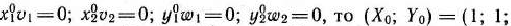
0; 0) является седловой точкой функции Лагранжа для исходной задачи. Следовательно,
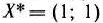
оптимальный план исходной задачи и
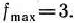
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
