Задача 3.12.
По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве изделий I способом затраты равны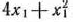 
руб., а при изготовлении 
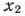изделий II способом они составляют 
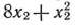руб. Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.
Решение:
Математическая постановка задачи состоит в определении минимального значения функции
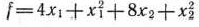
при условиях
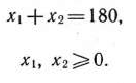
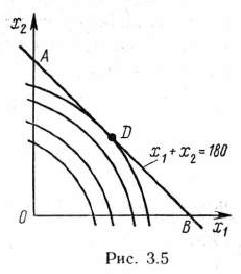
Сначала найдем решение задачи, используя ее геометрическую интерпретацию. Областью допустимых решений исходной задачи является отрезок прямой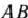 
(рис. 3.5), а линиями уровня — окружности с центром в точке 
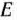(— 2; — 4).
Проводя из точки 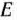окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке 
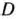. Чтобы найти координаты этой точки, воспользуемся тем, что угловой коэффициент к окружности
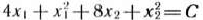
в точке 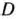совпадает с угловым коэффициентом прямой 
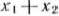= 180 и, следовательно, равен —1. Рассматривая 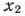как потную функцию от 
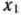и дифференцируя уравнение окружности, имеем
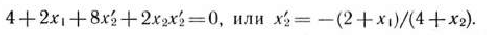
Приравнивая полученное выражение числу —1, получаем одно из уравнений для определения координат точки 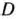. Присоединяя к нему уравнение прямой, на которой лежит точка 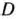, имеем систему
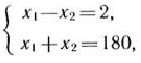
откуда
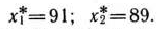
Это означает, что если предприятие изготовит 91 изделие I технологическим способом и 89 изделий II способом, то общие затраты будут минимальными и составят 17 278 руб.
Решим теперь задачу, используя метод множителей Ла-гранжа. Найдем минимальное значение функции (20) при условии (21), т. е. без учета требования неотрицательности переменных. Для этого составим функцию Лагранжа
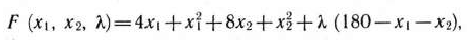
вычислим ее частные производные по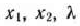 
и приравняем их нулю:
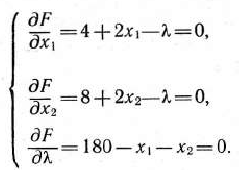
Перенося в правые части первых двух уравнений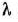 
и приравнивая их левые части, получим
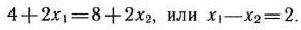
Решая последнее уравнение совместно с уравнением 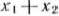= 180, находим
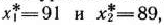
т. е. получили координаты точки 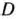, удовлетворяющей условиям (22). Эта точка является подозрительной на экстремум. Используя вторые частные производные, можно показать, что в точке 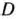функция 
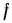имеет условный минимум. Этот результат и был получен выше.
Следует отметить, что такой же результат мы получим и в том Случае, если исследование на условный экстремум функции 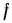сведем к исследованию на безусловный экстремум функции 
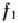полученной из 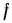в результате ее преобразований. А именно: если из уравнения связи (21) найдем 
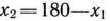и подставим это выражение и (20), то получим функцию одной переменной :
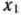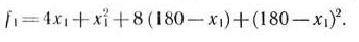
Найдем стационарную точку этой функции из уравнения
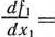
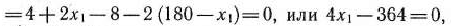
откуда
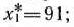
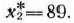
Так же как и выше, устанавливаем, что в данной точке функция 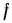имеет минимальное значение.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
