Задача 2.41.
Для выполнения работ могут быть использованы 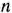 механизмов. Производительность
механизмов. Производительность 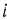 -го механизма
-го механизма 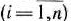 при выполнении
при выполнении 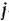 -й работы
-й работы 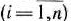 равна
равна 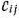 . Предполагая, что каждый механизм может быть использован только на одной работе и каждая работа может выполняться только одним механизмом, определить закрепление механизмов за работами, обеспечивающее; максимальную производительность. Построить математическую модель задачи.
. Предполагая, что каждый механизм может быть использован только на одной работе и каждая работа может выполняться только одним механизмом, определить закрепление механизмов за работами, обеспечивающее; максимальную производительность. Построить математическую модель задачи.
Решение:
Введем переменную 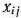 , значение которой равно 1, если при выполнении
, значение которой равно 1, если при выполнении 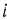 -й работы используется
-й работы используется 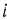 -й механизм, и равно 0 в противном случае. Тогда условия использования каждого механизма только на одной работе выражаются равенствами
-й механизм, и равно 0 в противном случае. Тогда условия использования каждого механизма только на одной работе выражаются равенствами
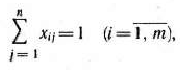
а условия выполнения работы только одним механизмом — равенствами
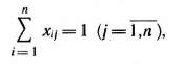

Таким образом, задача состоит в определении таких значении неизвестных 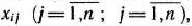 удовлетворяющих системам уравнений (28) и (29) и условию (30), при которых достигается максимальное значение функции
удовлетворяющих системам уравнений (28) и (29) и условию (30), при которых достигается максимальное значение функции
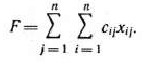
Сформулированная задача является задачей целочисленного программирования.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

