Задача 2.19.
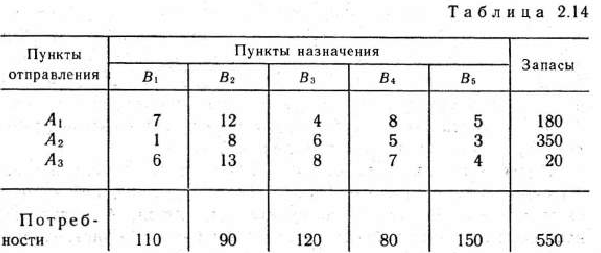
Для транспортной задачи, исходные данные которой приведены в табл. 2.14, найти оптимальный план методом дифференциальных рент.
Решение:
Перейдем от табл. 2.14 к табл. 2.15, добавив один дополнительный столбец для указания избытка и недостатка по строкам и одну строку для записи соответствующих разностей.
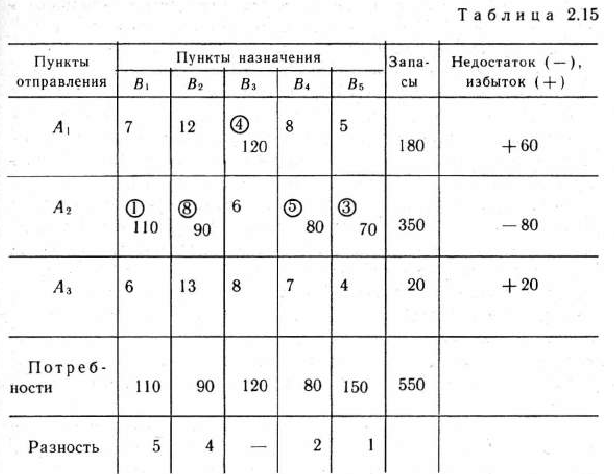
В каждом из столбцов табл. 2.15 находим минимальные тарифы и обводим их кружками. Заполняем клетки, в которых стоят указанные числа. Для этого в каждую из клеток записываем максимально допустимое число. Например, в клетку, находящуюся на пересечении строки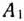 
и столбца 
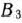записываем число 120. В эту клетку нельзя поместить большее число, поскольку в таком случае были бы превышены потребности пункта назначения .
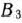В результате заполнения отмеченных выше клеток получен так называемый условно оптимальный план, согласно которому полностью удовлетворяются потребности пунктов назначения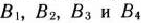 
и частично—пункта назначения 
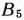. При этом полностью распределены запасы пункта отправления 
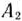, частично—пункта отправления 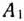и остались совсем нераспределенными запасы пункта отправления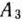 
После получения условно оптимального плана определяем избыточные и недостаточные строки. Здесь недостаточной является строка 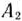, так как запасы пункта отправления 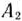полностью использованы, а потребности пункта назначения 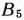удовлетворены частично. Величина недостатка равна 80 ед.
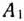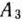Строки и являются избыточными, поскольку запасы пунктов отправления 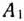и 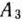. распределены не полностью. При этом величина избытка строки 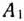равна 60 ед., а строки 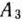—20 ед. Общая величина избытка 60 + 20 = 80 совпадает с общей величиной недостатка, равной 80.
После определения избыточных и недостаточных строк по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках. В данном случае эти разности соответственно равны 5, 4, 2, 1 (табл. 2.15). Для столбца 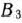разность не определена, так как число, записанное в кружке в данном столбце, находится в положительной строке. В столбце 
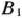число, стоящее в кружке, равно 1, а в избыточных строках в клетках данного столбца наименьшим является число 6. Следовательно, разность для данного столбца равна 6—1=5. Аналогично находим разности для других столбцов:
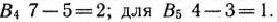
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце 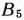. Найдя промежуточную ренту, переходим к табл. 2.16.
В этой таблице в строках 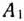и 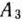(являющихся избыточными) переписываем соответствующие тарифы из строк 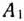и 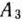табл. 2.15. Элементы строки 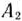(которая была недостаточной) получаются в результате прибавления к соответствующим тарифам, находящимся в строке 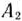табл. 2.15, промежуточной ренты, т. е. 1.
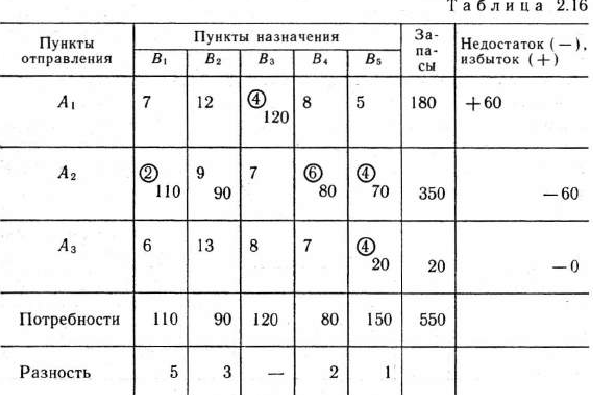
В табл. 2.16 число заполняемых клеток возросло на одну. Это обусловленно тем, что число минимальных тарифов, стоящих в каждом из столбцов данной таблицы, возросло на единицу, а именно в столбце 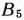теперь имеются два минимальных элемента 4. Эти числа заключаем а кружки; клетки, в которых они стоят, следует заполнить. Необходимо заполнить и клетки, в которых стоят наименьшие для других столбцов тарифы. Это клетки табл. 2.16, в которых соответствующие тарифы заключены в кружки. После того как указанные клетки определены, устанавливаем последовательность их заполнения. Для этого находим столбцы (строки), в которых имеется лишь одна клетка для заполнения. Определив и заполнив некоторую клетку, исключаем из рассмотрения соответствующий столбец (строку) и переходим к заполнению следующей клетки. В данном случае заполнение клеток проводим в такой последовательности. Сначала заполняем клетки 
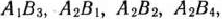, так как они являются единственными клетками для заполнения в столбцах 
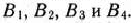После заполнения указанных клеток заполняем клетку 
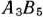, поскольку она является единственной для заполнения в строке 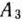. Заполнив эту клетку (табл. 2.16), исключаем из рассмотрения строку 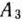. Тогда в столбце 65 остается лишь одна клетка для заполнения. Это клетка 
, которую заполняем. После заполнения клеток устанавливаем избыточные и недостаточные строки (табл. 2.16). Как видно из табл. 2.16, еще имеется нераспределенный остаток. Следовательно, получен условно оптимальный план задачи и нужно перейти к новой таблице. Для этого по каждому из столбцов находим разности между числом, записанным в кружке данного столбца, и наименьшим по отношению к нему числом, находящимся в избыточных строках (табл. 2.16). Среди этих разностей наименьшая равна 1. Это и есть промежуточная рента. Переходим к новой таблице (табл. 2.17).
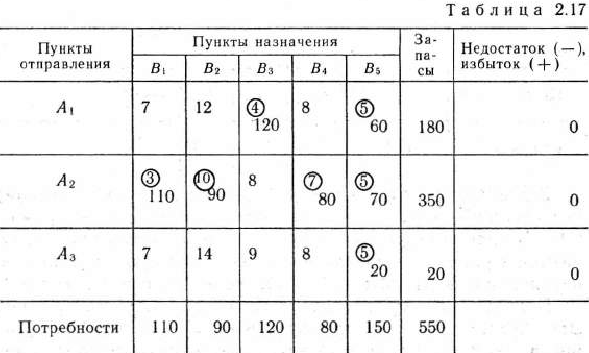
В новой таблице элементы строк 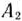и 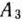получены в результате прибавления к соответствующим числам строк 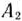и 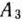(являющихся недостаточными) табл. 2.16 промежуточной ренты, т. е. 1. В результате в табл. 2.17 число клеток для заполнения возросло еще на одну и стало равным 6. Определяем указанные клетки и заполняем их. Сначала заполняем клетки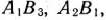 
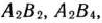, а затем 
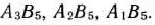. В результате все имеющиеся запасы поставщиков распределяются в соответствии с фактическими потребностями пунктов назначения. Число заполненных клеток равно 7, и все они имеют наименьший показатель 
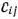. Следовательно, получен оптимальный план исходной транспортной задачи:
При этом плане перевозок общие затраты таковы:
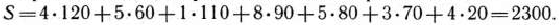
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
