Задача 2.9.
Найти опорный план транспортной задачи 2.1 методом минимального элемента.
Решение:
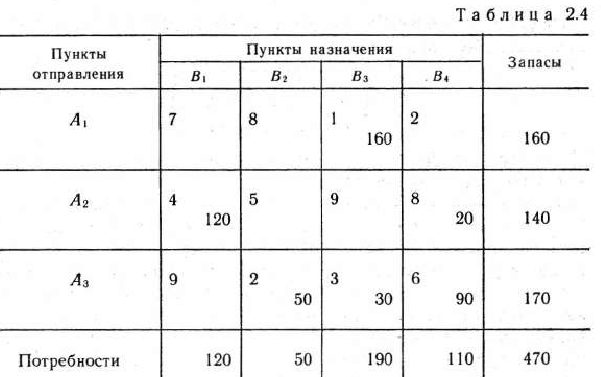
Исходные данные задачи запишем в виде табл. 2.4. Минимальный тариф, равный 1, находится в клетке для переменной  . Положим
. Положим  = 160, запишем это значение в соответствующую клетку табл. 2.4 и исключим временно из рассмотрения строку
= 160, запишем это значение в соответствующую клетку табл. 2.4 и исключим временно из рассмотрения строку 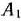 . Потребности пункта назначения
. Потребности пункта назначения 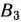 считаем равными 30 ед.
считаем равными 30 ед.
В оставшейся части таблицы с двумя строками 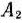 и
и 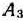 и четырьмя столбцами
и четырьмя столбцами 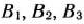 и
и 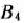 клетка с наименьшим значением тарифа
клетка с наименьшим значением тарифа 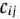 находится на пересечении строки и столбца
находится на пересечении строки и столбца 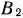 , где
, где 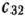 = 2. Положим
= 2. Положим 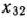 = 50 и внесем это значение в соответствующую клетку табл, 2,4.
= 50 и внесем это значение в соответствующую клетку табл, 2,4.
Временно исключим из рассмотрения столбец 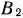 и будем считать запасы пункта
и будем считать запасы пункта 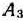 равными 120 ед. После этого рассмотрим оставшуюся часть таблицы с двумя строками
равными 120 ед. После этого рассмотрим оставшуюся часть таблицы с двумя строками 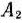 и
и 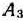 и тремя столбцами
и тремя столбцами 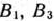 и
и 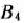 . В ней минимальный тариф
. В ней минимальный тариф 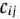 находится в клетке на пересечении строки
находится в клетке на пересечении строки 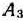 и столбца
и столбца 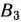 и равен 3. Запол-
и равен 3. Запол-
ним описанным выше способом эту клетку и аналогично заполним (в определенной последовательности) клетки, находящиеся на пересечении строки 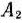 и столбца
и столбца 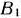 , строки
, строки 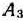 и столбца строки
и столбца строки 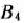 и столбца
и столбца 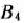 . В результате получим опорный план
. В результате получим опорный план

При данном плане перевозок общая стоимость перевозок составляет
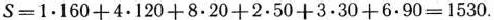
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

