Задача 1.105.
Найти максимальное значение функции
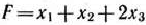
при условиях
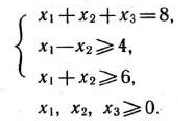
Решение:
Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции
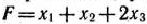
при условиях
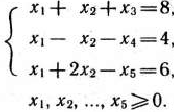
Умножим второе и третье уравнения системы ограничений последней задачи на —1 и переходим «следующей задаче: найти максимум функции
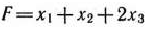
при условиях
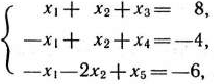
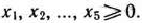
Составим для последней задачи двойственную. Такой является задача, в результате решения которой требуется найти минимальное значение функции
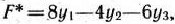
при условиях
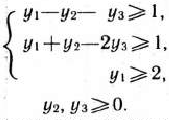
Выбрав в качестве базиса векторы 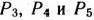 , составим симплексную таблицу (табл. 1.48) для исходной задачи (83) — (85).
, составим симплексную таблицу (табл. 1.48) для исходной задачи (83) — (85).

Из этой таблицы видим, что планом двойственной задачи (86) —(88) является 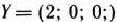 . При этом плане
. При этом плане 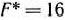 . Так как в столбце вектора
. Так как в столбце вектора 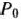 табл. 1.48 имеются два отрицательных числа (—4 и —6), а в 4-й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. (В данном случае это можно сделать, так как в строках векторов
табл. 1.48 имеются два отрицательных числа (—4 и —6), а в 4-й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. (В данном случае это можно сделать, так как в строках векторов 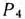 и
и 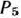 имеются отрицательные числа. Если бы они отсутствовали, то задача была бы неразрешима.) Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора
имеются отрицательные числа. Если бы они отсутствовали, то задача была бы неразрешима.) Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора 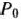 . В данном случае это число —6. Следовательно, из базиса исключаем вектор
. В данном случае это число —6. Следовательно, из базиса исключаем вектор 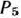 . Чтобы определить, какой вектор необходимо ввести в базис, находим
. Чтобы определить, какой вектор необходимо ввести в базис, находим 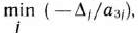 , где
, где 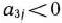 . Имеем
. Имеем
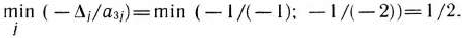
Значит, в базис вводим вектор 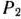 . Переходим к новой симплекс-таблице (табл. 1.49).
. Переходим к новой симплекс-таблице (табл. 1.49).
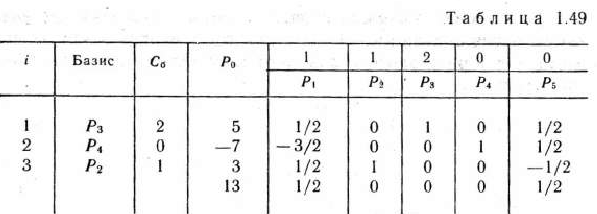
Из этой таблицы видно, что получен новый план двойственной задачи 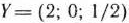 . При этом плане значение ее линейной формы равно
. При этом плане значение ее линейной формы равно 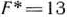 . Таким образом, с помощью алгоритма двойственного симплекс-метода произведен упорядоченный переход от одного плана двойственной задачи к другому.
. Таким образом, с помощью алгоритма двойственного симплекс-метода произведен упорядоченный переход от одного плана двойственной задачи к другому.
Так как в столбце вектора 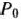 табл. 1.49 стоит отрицательное число —7, то рассмотрим элементы 2-й строки. Среди этих чисел есть одно отрицательное —3/2. Если бы такое число отсутствовало, то исходная задача была бы неразрешима. В данном случае переходим к новой симплекс-таблице (табл. 1.50).
табл. 1.49 стоит отрицательное число —7, то рассмотрим элементы 2-й строки. Среди этих чисел есть одно отрицательное —3/2. Если бы такое число отсутствовало, то исходная задача была бы неразрешима. В данном случае переходим к новой симплекс-таблице (табл. 1.50).
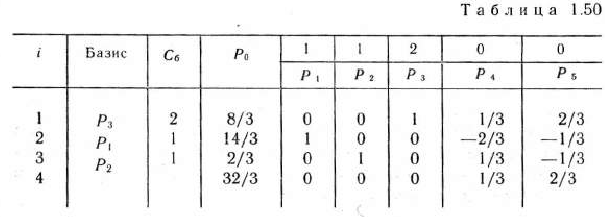
Как видно из табл. 1.50, найдены оптимальные планы исходной и двойственной задач. Ими являются
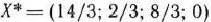
и
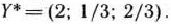
При этих планах значения линейных форм исходной и двойственной задач равны:
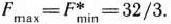
Задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

