Задача 1.89.
Для задачи, состоящей в определении максимального значения функции
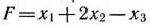
при условиях
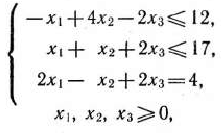
составить двойственную задачу и найти ее решение.
Решение:
Двойственная задача по отношению к исходной состоит в нахождении минимума функции
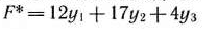
при условиях
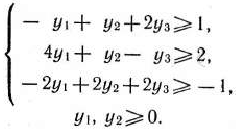
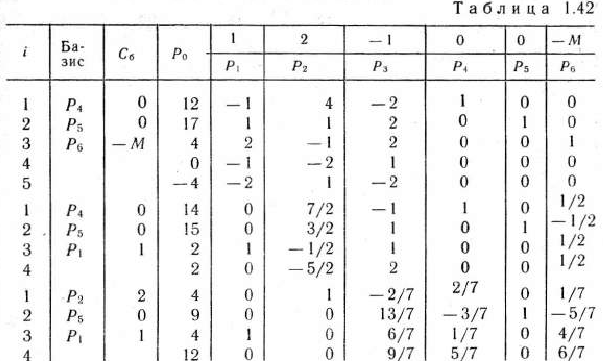
Чтобы найти решение двойственной задачи, сначала находим решение исходной задачи методом искусственного базиса. Оно приведено в табл. 1.42.
Из последней симплекс-таблицы видно, что двойственная задача имеет решение
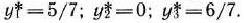
Оптимальные двойственные оценки удовлетворяют всем условиям двойственной задачи. При этом минимальное значение целевой функции двойственной задачи, равное
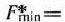
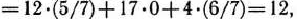
совпадает с максимальным значением целевой функции 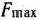 исходной задачи.
исходной задачи.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

