Задача 1.42.
Найти максимум функции
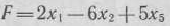
при условиях
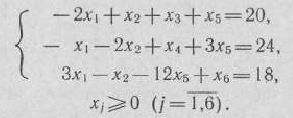
Решение:
Систему уравнений задачи запишем в векторной форме:
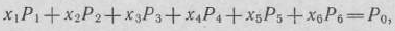
где
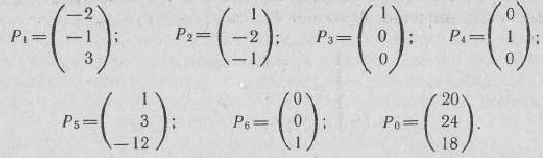
Так как среди векторов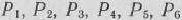 
имеется три единичных вектора, то для данной задачи можно непосредственно найти опорный план. Таковым является план 
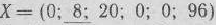, Составляем симплексную таблицу (табл. 1.10) и проверяем, является ли данный опорный план оптимальным.
Как видно из табл. 1.10, исходный опорный план не является оптимальным. Поэтому переходим к новому опорному плану. Это можно сделать, так как в столбцах векторов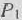 
и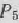 
, 4-я строка которых содержит отрицательные числа, имеются положительные элементы. Для перехода к новому опорному плану введем в базис вектор 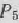и исключим из базиса вектор 
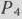. Составляем таблицу II итерации.
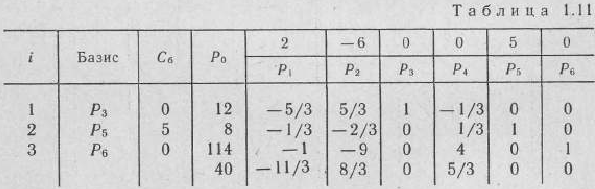
Как видно из табл. 1.11, новый опорный план задачи не является оптимальным, так как в 4-й строке столбца вектора 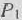стоит отрицательное число —11/3. Поскольку в столбце этого вектора нет положительных элементов, данная задача не имеет оптимального плана.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
