Задача 1.29.
Найти максимум и минимум функции
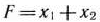
при условиях
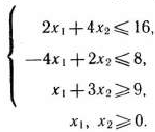
Решение:
Построим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств:
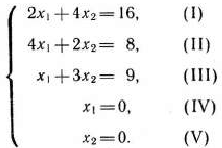
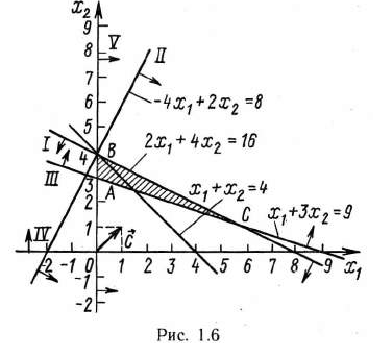
Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение (рис. 1.6).
Как видно из рис. 1.6, многоугольником решений задачи является треугольник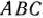 
. Координаты точек этого треугольника удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи. Следовательно, задача будет решена, если среди точек треугольника 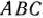найти такие, в которых функция 
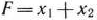принимает максимальное и минимальное значения. Для нахождения этих точек постоим прямую 
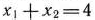(число 4 взято произвольно) и вектор 
.
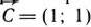Передвигая данную прямую параллельно самой себе в направлении вектора 
, видим, что ее последней общей точкой с многоугольником решений задачи является точка 
. Следова-
тельно, в этой точке функция 
принимает максимальное значение. Так как 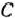— точка пересечения прямых I и II, то ее координаты удовлетворяют уравнениям этих прямых:
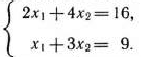
Решив эту систему уравнений, получим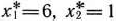 
. Таким образом, максимальное значение функции 
.
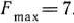Для нахождения минимального значения целевой функции задачи передвигаем прямую 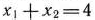в направлении, противоположном направлению вектора 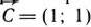. В этом случае, как видно из рис. 1.6, последней общей точкой прямой с многоугольником решений задачи является точка 
. Следовательно, в этой точке функция принимает минимальное значение. Для определения координат точки 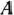решаем систему уравнений
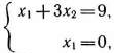
откуда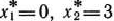 
. Подставляя найденные значения переменных в целевую функцию, получим 
.
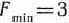Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
