Минимальные значения критериев на множестве эффективных точек
Для того чтобы определить минимальное значение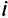 
-го критерия на эффективном множестве 
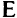, надо решить следующую задачу:
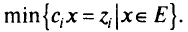
Поскольку эффективное множество 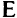неизвестно в явном виде, то непосредственно решить эту задачу нельзя. Причем для большинства задач МКЛП множество 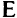не является выпуклым.
Один из способов решения поставленной задачи базируется на таблице выигрышей (табл. 5.12).
Строки таблицы выигрышей представляют собой критериальные векторы, полученные в результате максимизации отдельных критериев. В том случае, когда оптимум не единственный, требуется принять специальные меры, чтобы все критериальные векторы, стоящие в строках, были недоминируемыми. Величины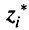 
, стоящие на главной диагонали, образовывают вектор максимальных значений критериев на множестве эффективных точек. Минимальное значение 
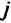-м столбце таблицы выигрышей — это некоторая оценка минимального значения 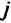-го критерия на множестве Е. Если минимальное по столбцу значение находится в строке, в которой стоит доминируемый критериальный вектор, то оно может оказаться меньше искомого минимума на множестве Е. Если строка, содержащая минимальное значение, является недоминируемым критериальным вектором, минимальное значение будет либо правильно определять минимальное значение критерия на множестве Е, либо будет его оценкой сверху. Но в целом этот подход ненадежен.
Для определения на множестве эффективных точек минимального значения 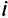-го критерия можно использовать симплекс-метод. Поочередно лексикографически максимизируя каждый из критериев, строим таблицу выигрышей. Пусть 
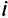— минимальное значение критерия в -м столбце таблицы выигрышей. Добавим в условия-ограничения задачи еще одно ограничение: 
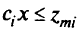. Начнем счет с крайней точки, соответствующей . Исследуем грань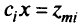 
, нового (после дополнительного ограничения) множества допустимых точек с целью найти такую крайнюю точку, из которой исходит эффективное ребро с убывающим значением 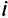-го критерия. Если такого ребра нет, то текущее значение zmi и есть минимальное значение 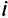-го критерия на процесс окончен. Если такое ребро существует, то производим замещение вдоль этого ребра методом Жордана и переходим в крайнюю точку на другом его конце, где значение 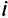-го критерия равно 
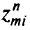. Вводим дополнительное ограничение 
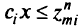и повторяем процедуру. Алгоритм заканчивает работу в точке минимума 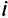-го критерия на множестве эффективных точек.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Метод взвешенных сумм с точечным оцениванием весов |
| Сжатие множества допустимых решений |
| Параметризация целевой функции |
| Целевое программирование |
