Оглавление:
Комбинированный метод внутренней и внешней точек
Введем новый параметр
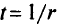
и рассмотрим комбинированную функцию
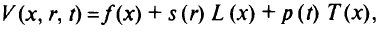
где 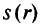 — функция от
— функция от 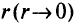 для метода внутренней точки;
для метода внутренней точки; 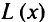 — функция штрафа для метода внутренней точки;
— функция штрафа для метода внутренней точки; 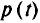 — функция от
— функция от 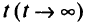 для метода внешней точки;
для метода внешней точки; 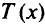 — функция штрафа для метода внешней точки.
— функция штрафа для метода внешней точки.
Покажем на примере, как применяется комбинированная функция 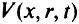 для решения задачи математического программирования.
для решения задачи математического программирования.
Пример:
Минимизировать
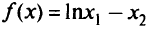
при ограничениях
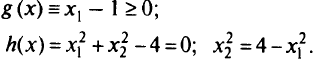
Решение:
Построим комбинированную функцию
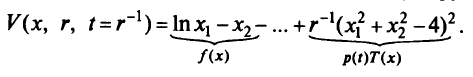
С помощью комбинированной функции мы избежали использования модулей 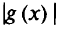 , которые появляются в методе внешней точки. Необходимые условия минимума функции
, которые появляются в методе внешней точки. Необходимые условия минимума функции 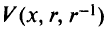 дают
дают
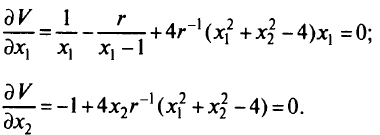
Отсюда
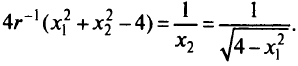
Зададим последовательность значений 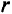 : 1,0; 1/4; 1/16; 1/64; 1/256 и получим соответствующие ей последовательности значений:
: 1,0; 1/4; 1/16; 1/64; 1/256 и получим соответствующие ей последовательности значений:

Последовательности значений 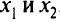 дают оптимальное решение
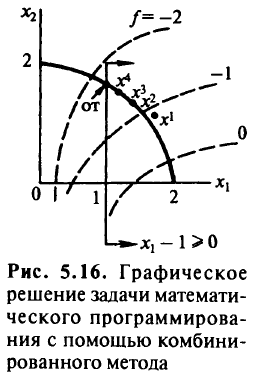
дают оптимальное решение 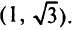 Графическое решение задачи математического программирования приведена на рис 5.16.
Графическое решение задачи математического программирования приведена на рис 5.16.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

