Оглавление:
Методы внутренней точки для задачи математического программирования
Рассмотрим общую задачу математического программирования, не содержащую ограничений в виде равенств, т.е. минимизировать 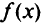 при ограничениях
при ограничениях
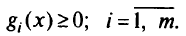
Пусть вблизи локального минимума этой задачи 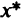 существует окрестность, где есть такая точка
существует окрестность, где есть такая точка 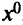 в которой
в которой
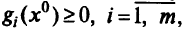
и выполняются условия строгой дополняющей нежесткости:
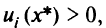
если
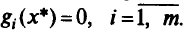
Видоизменим достаточные условия локального минимума в точке 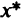 , сформулированные в разд. 1.5. Предположим, что при малом
, сформулированные в разд. 1.5. Предположим, что при малом 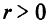 в точке
в точке 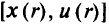 вблизи точки
вблизи точки 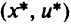 выполняются условия:
выполняются условия:
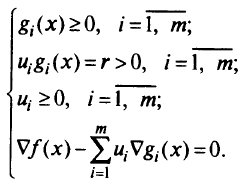
Из второго условия выразим 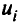 и подставим это выражение в последнее равенство:
и подставим это выражение в последнее равенство:
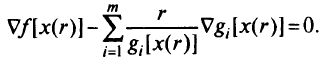
Непосредственной проверкой легко установить, что левая часть этого выражения — это градиент функции
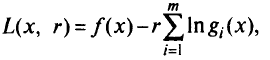
обращающийся в нуль в точке 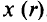 , причем
, причем 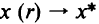 при
при  . Функцию
. Функцию 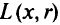 в таком виде называют логарифмической штрафной. Аналогично получаем другой вид штрафной функции
в таком виде называют логарифмической штрафной. Аналогично получаем другой вид штрафной функции 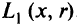 полагая
полагая
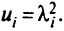
При условии, что
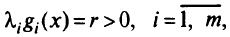
имеем
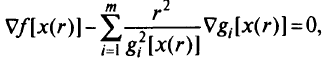
и функция
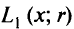
примет вид
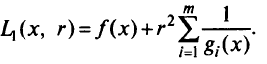
Задавая последовательность значений 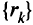 , стремящуюся к нулю, получаем последовательность
, стремящуюся к нулю, получаем последовательность 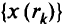 , сходящуюся к
, сходящуюся к 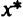 . С помощью новых функций
. С помощью новых функций 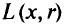 мы свели задачу определения условного экстремума (задачу математического программирования) к задаче поиска безусловного экстремума функции
мы свели задачу определения условного экстремума (задачу математического программирования) к задаче поиска безусловного экстремума функции 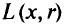 . Точнее, задачу математического программирования заменили семейством функций, зависящих от параметра r и обладающих следующими свойствами:
. Точнее, задачу математического программирования заменили семейством функций, зависящих от параметра r и обладающих следующими свойствами:
1) в окрестности оптимальной точки они близки к заданной минимизируемой функции;
2) каждая функция из построенного семейства достаточно быстро возрастает при приближении к границе допустимой области из «внутренней» части допустимой области.
К минимизируемой функции исходной задачи мы добавили ряд слагаемых, называемых штрафными (барьерными) функциями, зависящими от параметра r и функции одного из ограничений. При фиксированном значении параметра r второе слагаемое стремится к бесконечности при стремлении к нулю его аргумента. Каждую функцию семейства подвергают безусловной минимизации, и этот процесс не может вывести 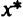 за пределы допустимой области. Подобные методы названы методами внутренней точки.
за пределы допустимой области. Подобные методы названы методами внутренней точки.
В задаче математического программирования при наличии ограничений-равенств допустимой области (в виде области) нет, и «метод внутренней точки» не применим.
Рассмотрим некоторые примеры перехода от задачи математического программирования к задаче безусловной минимизации «методом внутренней точки».
Пример:
Минимизировать
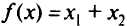
при ограничениях
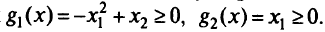
Решение:
Построим логарифмическую штрафную функцию
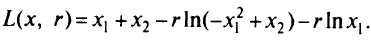
Определим точки минимума 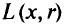 аналитически, так как
аналитически, так как 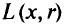 дифференцируема в рассматриваемой области. Для нахождения
дифференцируема в рассматриваемой области. Для нахождения 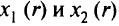 получим систему уравнений:
получим систему уравнений:
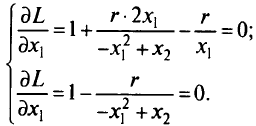
Отсюда найдем, что
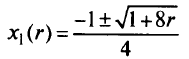
(здесь оставим только знак «+», так как 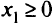 );
);
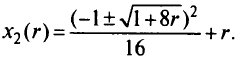
Заметим, что значения 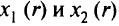 удовлетворяют условию положительной определенности матрицы
удовлетворяют условию положительной определенности матрицы 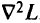 . Возьмем последовательность значений r: 1,0; 0,5; 0,25; 0,1. Соответственно получим последовательности значений
. Возьмем последовательность значений r: 1,0; 0,5; 0,25; 0,1. Соответственно получим последовательности значений
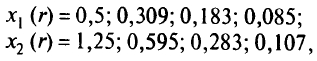
сходящиеся при r->0 к точке (0, 0). Графическое решение данной задачи представлено на рис. 5.14.
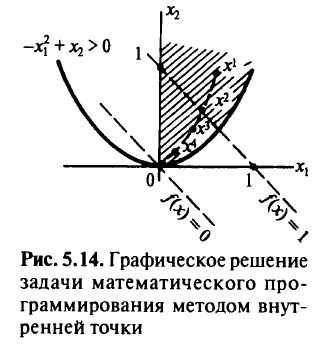
В общем случае в задачах со многими локальными минимумами (при слабых условиях регулярности) существует последовательность безусловных локальных минимумов, сходящихся к каждому из условных локальных минимумов.
Рассмотрим второй пример: решение задачи линейного программирования методом внутренней точки.
Пример:
Минимизировать 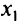 при условии
при условии
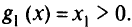
Решение:
Построим логарифмическую штрафную функцию
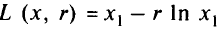
Необходимое условие существования минимума:
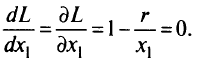
Отсюда находим, что
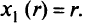
Из условия
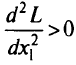
следует, что для
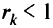
безусловный минимум будет при
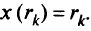
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

