Приложения задач о многопродуктовом потоке
Задачи о многопродуктовом потоке находят широкое применение при проектировании коммуникационных систем, осуществлении железнодорожных перевозок, планировании производства и распределения, в военном деле, а также в других областях. В насто-ящем разделе мы остановимся на нескольких приложениях многопродуктовых сетевых моделей и дадим новые формулировки некоторых задач о многопродуктовом потоке.
Составление расписания движения судов. Одной из наиболее часто возникающих задач в области планирования перевозок является задача составления оптимального расписания движения транспортных средств. Предположим, что известно число разнотипных судов, которые отличаются друг от друга скоростью передвижения, грузоподъемностью и эксплуатационными расходами. Функция полезности определяется размерами поставки груза отдельным судном к заданному сроку и затратами на осуществление соответствующей перевозки.
Кроме того, имеются затраты (отрицательная полезность), связанные с перегоном судна из порта, где оно было разгружено, в порт погрузки. Задача заключается в максимизации функции полезности путем составления оптимальных маршрутов и расписания движения судов.
Данная задача может быть сформулирована в виде следующей сетевой задачи. Каждый узел у сети соответствует прибытию судна в порт назначения в один из допустимых сроков доставки. Каждый узел 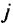 соответствует исходному порту и моменту, равному разности срока доставки и времени транспортировки, которое по предположению является детерминированным. Дуга
соответствует исходному порту и моменту, равному разности срока доставки и времени транспортировки, которое по предположению является детерминированным. Дуга 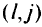 соответствует перевозке груза, а дуга
соответствует перевозке груза, а дуга 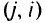 — перегону судна из порта доставки в исходный порт. Суда
— перегону судна из порта доставки в исходный порт. Суда 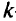 -го типа первоначально располагают в источнике
-го типа первоначально располагают в источнике 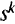 и дуги
и дуги 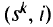 , таким образом, соответствуют началу их эксплуатации. Далее вводят фиктивный сток
, таким образом, соответствуют началу их эксплуатации. Далее вводят фиктивный сток 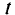 и дугу
и дугу 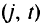 , соответствуюшие завершению эксплуатации судов. И наконец, суммарный поток перевозимого груза но всем лугам, соответствующим различным датам перевозки и типам судов, не должен превосходить некоторой заданной величины. Математически эта задача формулируется следующим образом: максимизировать
, соответствуюшие завершению эксплуатации судов. И наконец, суммарный поток перевозимого груза но всем лугам, соответствующим различным датам перевозки и типам судов, не должен превосходить некоторой заданной величины. Математически эта задача формулируется следующим образом: максимизировать
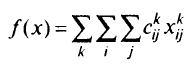
при условии, что
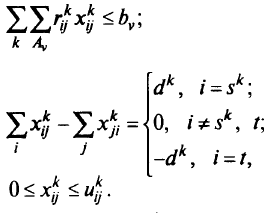
Здесь через 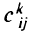 обозначена полезность, соответствующая отдельному судну, перевозимому грузу и маршруту;
обозначена полезность, соответствующая отдельному судну, перевозимому грузу и маршруту; 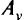 — это множество допустимых маршрутов для данного груза;
— это множество допустимых маршрутов для данного груза; 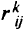 — грузоподъемность судна
— грузоподъемность судна 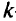 -го типа на маршруте
-го типа на маршруте 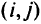 . Суммарный перевозимый груз не может превышать спроса на него
. Суммарный перевозимый груз не может превышать спроса на него 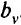 . Ограничения (5.12) описывают условие сохранения потока по числу судов
. Ограничения (5.12) описывают условие сохранения потока по числу судов 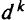 , а величина
, а величина 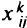 равна 0 или
равна 0 или  в зависимости от того, может ли быть использовано на дуге
в зависимости от того, может ли быть использовано на дуге 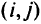 судно
судно 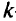 -го типа или нет.
-го типа или нет.
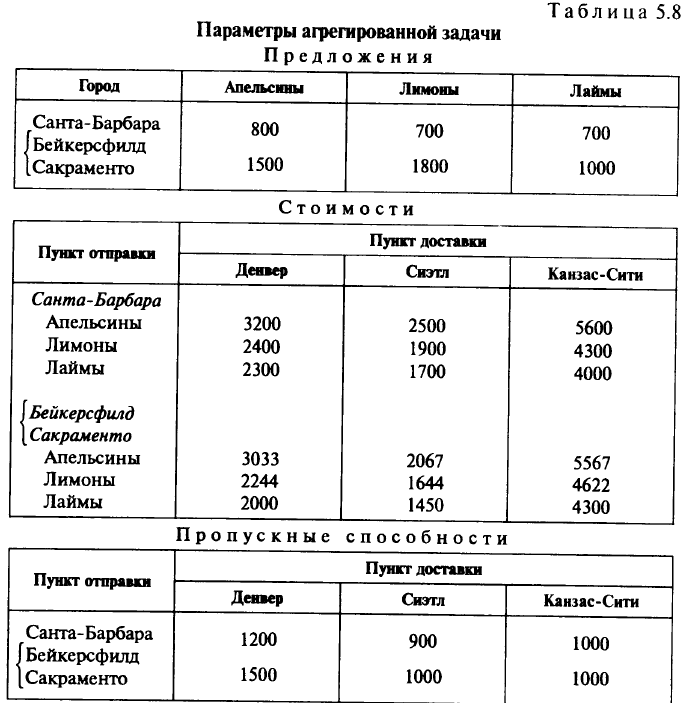
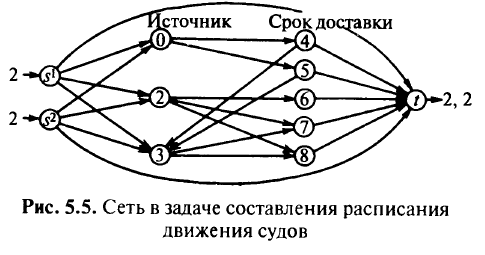
В качестве примера рассмотрим задачу, описанную в табл. 5.9. Число судов каждого типа равно 2. Соответствующая сеть изображена на рис. 5.5. Отметим, что в таком классе задач узлы служат для обозначения места и времени.

Проектирование городской транспортной сети. Многопродуктовые сетевые модели используют и при проектировании городских транспортных сетей. В этих моделях узлы соответствуют участкам или районам города, а дуги — улицам или дорогам других видов. Требования к транспортной сети задаются матрицей поездок 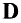 , элементы
, элементы 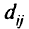 которой равны числу транспортных средств, движущихся из участка
которой равны числу транспортных средств, движущихся из участка 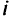 к участку
к участку 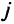 в течение фиксированного интервала времени. Каждая дуга имеет заданную пропускную способность и,
в течение фиксированного интервала времени. Каждая дуга имеет заданную пропускную способность и,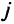 которая может быть увеличена (например, в результате улучшения дорог). Плата за увеличение пропускной способности дуги
которая может быть увеличена (например, в результате улучшения дорог). Плата за увеличение пропускной способности дуги 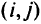 на единицу равна
на единицу равна 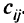 . Общая сумма денежных средств, предназначенных на улучшение дорог, равна В. «Продуктами» в данной модели являются потоки из каждого источника во все пункты назначения. Пусть
. Общая сумма денежных средств, предназначенных на улучшение дорог, равна В. «Продуктами» в данной модели являются потоки из каждого источника во все пункты назначения. Пусть 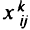 — число транспортных средств, движущихся по дуге
— число транспортных средств, движущихся по дуге 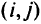 и начавших свой пусть в узле
и начавших свой пусть в узле 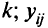 — увеличение пропускной способности дуги
— увеличение пропускной способности дуги 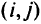 Предположим, что время проезда по дуге
Предположим, что время проезда по дуге 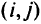 является некоторой функцией потока:
является некоторой функцией потока:
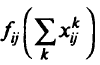
Задача проектирования сети заключается в определении дуг, пропускную способность которых следует увеличить, и вычислении потоков по каждой дуге, минимизирующих общее время поездки. Математически данная задача формулируется следующим образом:
минимизировать
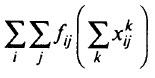
при условии, что
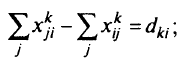
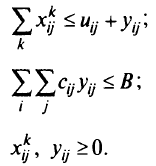
В задаче (5.14) было сделано одно важное допущение, касающееся поведения водителя. Оно основано на классическом принципе распределения транспортных средств: водители выбирают маршруты таким образом, что суммарное время поездок для всей системы является минимальным. Как правило, целевая функция задачи (5.14) является нелинейной и выпуклой.
Модели вычислительных систем. Очень похожи на только что рассмотренную нами модель городской транспортной сети многие модели вычислительных систем. В этих моделях дуги соответствуют каналам, а узлы — терминалам, системным и запоминающим устройствам и т.п. Каждая дуга имеет фиксированную пропускную способность 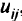 , которая может быть увеличена на
, которая может быть увеличена на 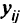 единиц вплоть до максимального значения
единиц вплоть до максимального значения 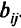 . Стоимость увеличения пропускной способности на единицу равна
. Стоимость увеличения пропускной способности на единицу равна 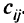 . Роль продуктов вновь играют потоки (информация) из источника во все пункты назначения, а вместо матрицы поездок
. Роль продуктов вновь играют потоки (информация) из источника во все пункты назначения, а вместо матрицы поездок 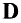 вводят матрицу, элементы
вводят матрицу, элементы 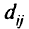 которой соответствуют объему информации, передаваемой из узла
которой соответствуют объему информации, передаваемой из узла 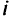 в узел
в узел 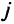 . Стоимость передачи единицы информации по дуге
. Стоимость передачи единицы информации по дуге 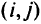 равна
равна 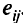 . Математически эта задача может быть сформулирована следующим образом:
. Математически эта задача может быть сформулирована следующим образом:
минимизировать
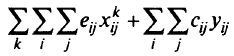
при условии, что
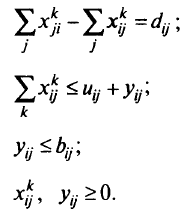
Описанная модель может быть использована для определения пропускной способности каналов, при которой заданные требования удовлетворяются с минимальными затратами. В этом случае значения 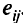 обычно полагают равными 0, если
обычно полагают равными 0, если 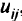 =0, а величины
=0, а величины 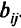 выбирают достаточно большими. Другим примером использования этой модели является задача минимизации стоимости передачи информации при фиксированных пропускных способностях дуг. В этом случае
выбирают достаточно большими. Другим примером использования этой модели является задача минимизации стоимости передачи информации при фиксированных пропускных способностях дуг. В этом случае 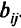 = 0.
= 0.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

