Многопродуктовые потоки в сетях
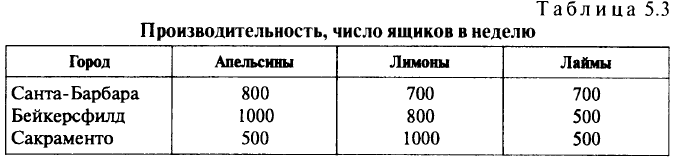
Существует немало практических задач о перевозке нескольких различных продуктов, которые должны сохраняться при прохождении по дугам сети. Необходимо иметь возможность различать продукты. Рассмотрим, например, упрошенную задачу транспортировки грех видов фруктов из садов, расположенных в Калифорнии, в магазины, ведущие оптовую торговлю. Предположим, что сады расположены в городах Санта-Барбара, Бейкерсфилд и Сакраменто. В период уборки урожая из этих садов поставляют в различных количествах апельсины, лимоны и лаймы (табл. 5.3).
По договорному соглашению требуется доставлять в оптовые магазины, расположенные в Денвере, Сиэтле и Канзас-Сити, количество фруктов, указаное в табл. 5.4. Перевозка осуществляется по железной дороге, однако в каждом поезде для фруктов отведено
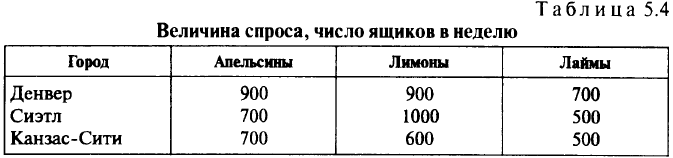
ограниченное место. Пропускные способности путей между различными пунктами отправления и пунктами назначения приведены в табл. 5.5. Независимо от вида фруктов данные
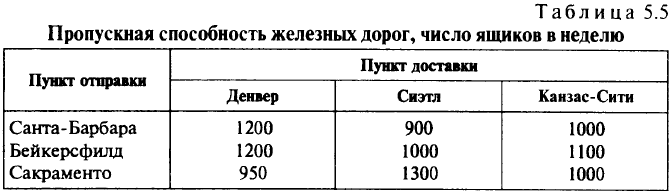
величины задаются числом ящиков, перевозимых в неделю (предполагается, что все фрукты упакованы в ящики одинаковых размеров). Вес каждого ящика, а следовательно, и соответствующие транспортные затраты зависят от вида упакованных в него фруктов. Затраты на транспортировку одного ящика приведены в табл. 5.6.
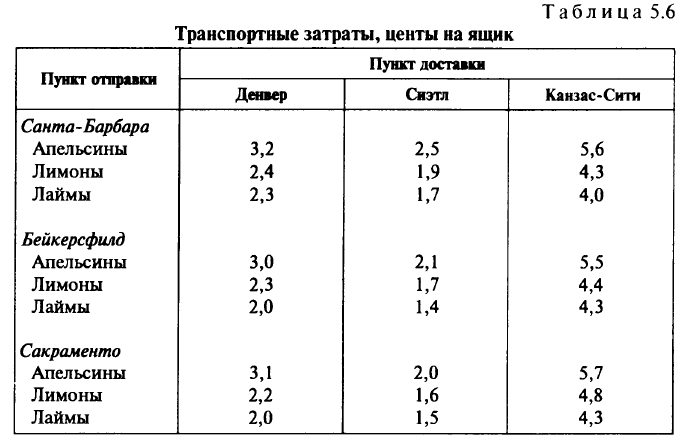
Задача определения схемы перевозки фруктов, минимизирующей транспортные затраты, является задачей о многопродуктовом потоке. Характерная особенность такой задачи в том, что по дугам сети протекает несколько неоднородных потоков. При этом суммарный поток всех продуктов по дуге ограничен ее пропускной способностью. Если бы это было не так, то можно было бы для каждого продукта независимо решить минимизационную транспортную задачу. Однако указанные выше ограничения на пропускные способности дуг существенно усложняют решение задачи.
Задачи о многопродуктовом потоке, как и об однопродуктовом потоке, могут быть сформулированы в виде задач линейного программирования. Задача о транспортировке фруктов является примером многопродуктовой транспортной задачи. Обозначим через
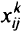поток 
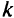-го продукта из 
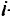-го источника в 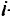-й сток, а через 
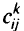— стоимость транспортировки единицы этого продукта. Пусть далее 
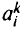и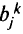 
— это соответственно предложение узла 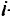и спрос узла 
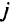для 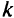-го продукта, а 
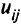— пропускная способность дуги 
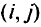. Математическая постановка многопродуктовой транспортной задачи выглядит следующим образом: минимизировать
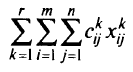
при условии, что
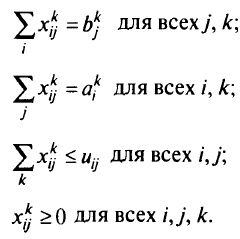
Как и в однопродуктовой транспортной задаче, предполагается, что для каждого продукта суммарное предложение равно суммарному спросу, т.е.
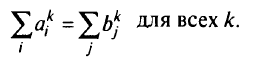
Во многих задачах, называемых многопродуктовыми задачами о перевозках, вводят промежуточные узлы, т. е. такие узлы, которым не приписывают ни спрос, ни предложение, а только требуют, чтобы для них выполнялось условие сохранения потока.
В качестве одного из таких примеров рассмотрим сеть, изображенную на рис. 5.2. Узлы 1 и 2 являются источниками 1 -го продукта, а узел 2 — источником 2-го продукта. Узел 5 является пунктом назначения для обоих продуктов, а узлы 3 и 4 — промежуточными. Многопродуктовая задача о перевозках может быть сформулирована в виде следующей задачи линейного программирования:
минимизировать
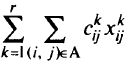
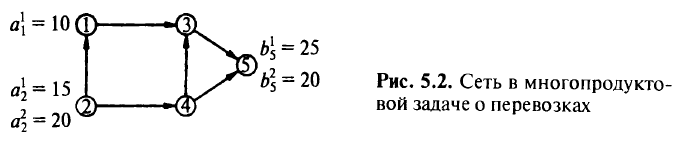
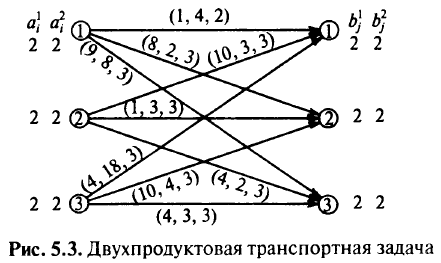
при условии, что
Через А здесь обозначается множество дуг сети.
Одна из трудностей решения задачи о многопродуктовом потоке вызвана тем, что оптимальные решения могут быть нецелочисленными. В качестве примера рассмотрим двухпродуктовуютранспортную задачу, сетевая формулировка которой задана на рис. 5.3. Дугам сети приписаны числа
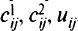
Оптимальное решение соответствующей задачи линейного программирования представлено в табл. 5.7.
Нецелочисленные решения возникают по той причине, что матрицы ограничений в задачах линейного программирования, вообще говоря, не унимодулярны. Напомним, что условие унимодулярности матрицы ограничений является достаточным для существования целочисленных оптимальных решений. Поскольку в задачах об однопродуктовом потоке данное условие выполнено, то для них можно разработать высокоэффективные алгоритмы, в которых по существу выполняются только две операции —
сложение и вычитание, а такие операции, как, например, деление и обращение матрицы, не требуются. С вычислительной точки зрения арифметические операции с целыми числами выполняются намного быстрее, чем операции, использующие числа (десятичные) с плавающей точкой. Благодаря этому создают программы, позволяющие очень быстро решать задачи большой размерности.
Для задач о многопродуктовом потоке были разработаны специальные алгоритмы, в которых учтены специфика структуры и свойства данного класса задач. Было показано, что эти алгоритмы являются более быстрыми, чем процедуры решения обшей задачи линейного программирования, но значительно более медленными, чем соответствующие алгоритмы задач об однопродуктовом потоке. Детальное изучение этих методов выходит за рамки нашей книги. Однако в настоящей главе мы рассмотрим ряд специальных вопросов, связанных с задачами о многопродуктовом потоке и методами их решения.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
