Понятие о параметрическом программировании
Исходные данные, необходимые для численной постановки реальных задач математического программирования, определяют в большинстве случаев неточно, приближенно. Это связано не только с наличием погрешностей измерения, но и с желанием описать в математической постановке возможное изменение исходных данных, чтобы в дальнейшем для оптимизации решения использовать наилучшие их значения.
Исследование чисто математических проблем, таких как анализ чувствительности решения при вариации исходных данных, оценка устойчивости решения, также требует разработки методов, учитывающих неопределенность исходных данных.
Как было показано, наиболее развиты к настоящему времени и наиболее доступны для изучения задачи линейного программирования. Алгоритм учета неопределенности исходных данных мы рассмотрим на примере задач линейного программирования, так как в других случаях учет неопределенности может оказаться крайне трудной проблемой. Раздел математического программирования, в котором может быть решена данная проблема, называют параметрическим программированием. Параметрическое программирование изучает в основном задачи, которые являются естественным обобщением задач линейного программирования, когда исходные данные (коэффициенты) в целевой функции и в условиях-ограничениях предполагаются не постоянными величинами, а функциями, зависящими определенным образом (чаще всего линейно) от некоторых параметров. Всякой задаче параметрического программирования можно поставить в соответствие некоторую задачу линейного программирования, называемую исходной. От того, как именно трактуется исходная задача, зависит трактовка параметрической задачи. Введение параметра обычно отражает некоторую реальную ситуацию.
Приведем несколько постановок задач параметрического программирования, которые наиболее естественным образом могут быть сопоставлены с принятой исходной задачей. Рассмотрим, помимо этого, одну из интерпретаций задачи параметрического программирования.
Пусть коэффициенты целевой функции исходной задачи линейного программирования (2.2) зависят от одного параметра. В задаче (2.2) коэффициенты целевой функции представляют собой цену единицы количества некоторого продукта, а координаты векторов-ограничений могутбыть истолкованы как запасы различных ресурсов.
Целевая функция рассматриваемой задачи параметрического программирования может иметь (в простейшем случае) следующий вид:
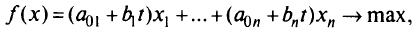
где 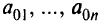 — исходные (старые) коэффициенты задачи линейного программирования;
— исходные (старые) коэффициенты задачи линейного программирования; 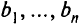 — новые коэффициенты;
— новые коэффициенты; 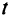 — параметр,
— параметр, 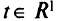 .
.
Зависимость коэффициентов этой функции от параметра 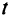 можно понимать как зависимость цены единицы продукта от времени. Различные новые коэффициенты
можно понимать как зависимость цены единицы продукта от времени. Различные новые коэффициенты 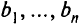 отражают индивидуальный характер зависимости от параметра
отражают индивидуальный характер зависимости от параметра 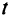 цен разных продуктов. Значение целевой функции исходной задачи равно стоимости выпущенной продукции, а значение целевой функции соответствующей параметрической задачи показывает, чему равна стоимость выпускаемой продукции при условии изменения цены единицы продукции, когда закон изменения этих цен (от времени, от качества продукции и т. п.) задан.
цен разных продуктов. Значение целевой функции исходной задачи равно стоимости выпущенной продукции, а значение целевой функции соответствующей параметрической задачи показывает, чему равна стоимость выпускаемой продукции при условии изменения цены единицы продукции, когда закон изменения этих цен (от времени, от качества продукции и т. п.) задан.
Рассмотрим случай, когда от параметра зависят координаты системы ограничений. Можно учесть зависимость этих показателей от времени, способа выработки ресурса, района размещения объекта, модель которого рассматривается в задаче и т. п. Условия-ограничения примут вид:
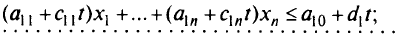
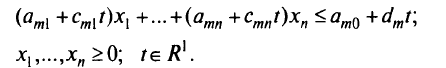
Буквой 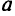 с соответствующими индексами обозначены исходные коэффициенты в условиях-ограничениях задачи, а буквами
с соответствующими индексами обозначены исходные коэффициенты в условиях-ограничениях задачи, а буквами 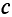 и
и 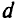 — новые коэффициенты, определяющие зависимость исходных коэффициентов от параметра
— новые коэффициенты, определяющие зависимость исходных коэффициентов от параметра 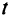 .
.
Задача параметрического программирования с 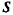 независимыми переменными
независимыми переменными  , или
, или 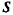 -параметрическая задача, записывается следующим образом: максимизировать
-параметрическая задача, записывается следующим образом: максимизировать
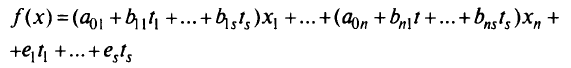
при ограничениях
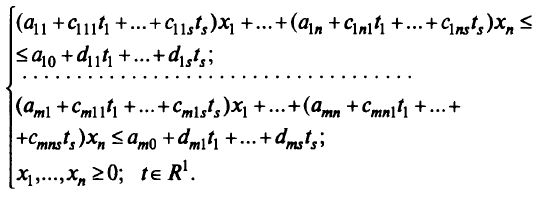
Рассмотрим метод решения частной задачи линейного параметрического программирования, в которой все коэффициенты целевой функции линейно зависят от некоторого действительного параметра  , на конкретном примере:
, на конкретном примере:
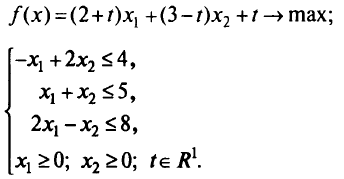
В матрично-векторной форме:
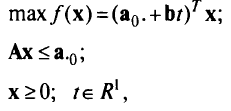
где
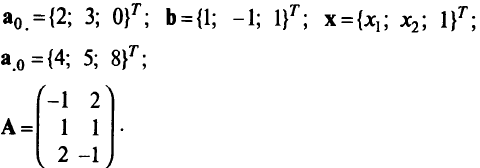
Для каждого фиксированного значения 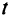 задача (5.1) становится задачей линейного программирования, которую называют принадлежащей этому значению
задача (5.1) становится задачей линейного программирования, которую называют принадлежащей этому значению 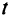 .
.
Решением параметрической задачи (5.1) называют явным образом заданную функцию
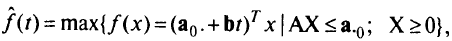
решающую функцию задачи (5.1), вместе с набором решающих отношений
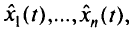
каждое из значений которых при данном значении 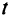 равно значениям переменных
равно значениям переменных
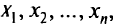
образующих оптимальное решение задачи, принадлежащей данному значению 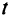 (если это решение существует). Доказано, что
(если это решение существует). Доказано, что 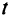 -я критическая область
-я критическая область 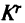 задачи (5.1),
задачи (5.1),
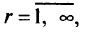
определяемая условием
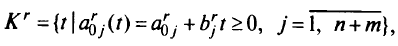
является отрезком (замкнутым интервалом). Область определения 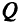 решающей функции
решающей функции 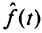 выпукла; решающая функция
выпукла; решающая функция 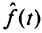 выпукла в своей области определения.
выпукла в своей области определения.
При любом 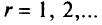 Для всех значений t из критической области решающая функция линейна и в силу этого непрерывна в области множества значений отношений
Для всех значений t из критической области решающая функция линейна и в силу этого непрерывна в области множества значений отношений
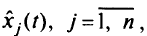
ограничены постоянными величинами; сами эти отношения полунепрерывны сверху.
Для построения решающей функции будем пользоваться симплекс-методом в следующей его модификации. Под последней строкой первой из симплекс-таблиц, полученной при 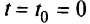 и содержащей некоторое допустимое базисное решение, приписывают еще одну строку коэффициентов
и содержащей некоторое допустимое базисное решение, приписывают еще одну строку коэффициентов
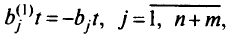
где
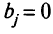
для
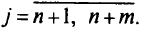
Полученная строка подвергается тем же преобразованиям, что и остальные (табл. 5.1; 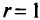 ). Естественно, что в задаче (5.1) мы предварительно перешли к ограничениям-равенст-
). Естественно, что в задаче (5.1) мы предварительно перешли к ограничениям-равенст-
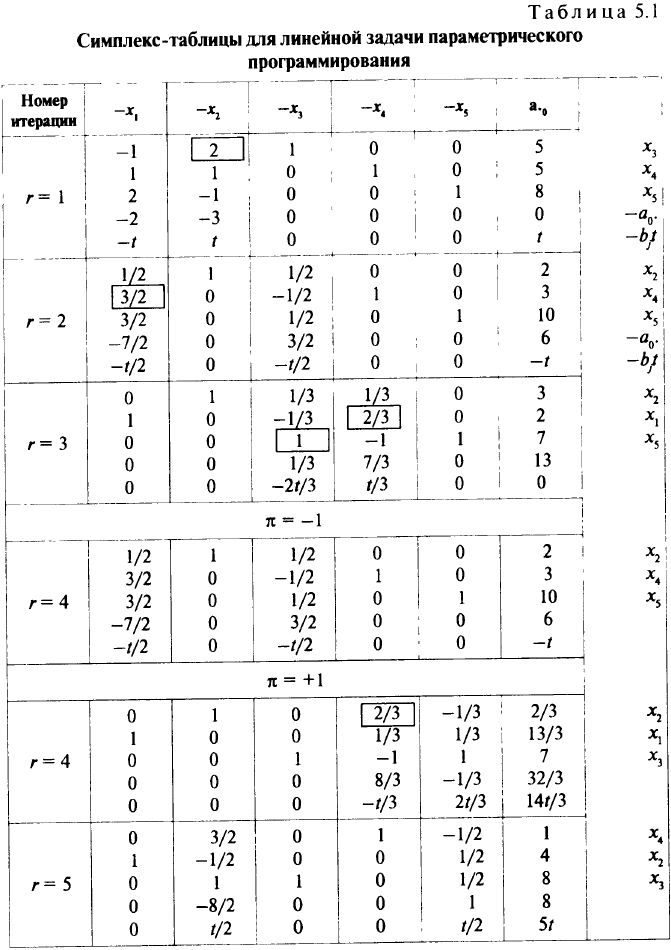
вам и ввели новые переменные 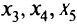 . Затри итерации
. Затри итерации 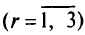 мы получили оптимальное решение при
мы получили оптимальное решение при 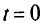 (в табл. 5.1 для каждой итерации выделены разрешающие элементы).
(в табл. 5.1 для каждой итерации выделены разрешающие элементы).
Коэффициенты в целевой функции для выбора разрешающего элемента задаются двумя последними строками при фиксированном (заданном) значении 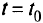 . Для данного допустимого базисного решения надо построить соответствующую критическую область — множество всех значений
. Для данного допустимого базисного решения надо построить соответствующую критическую область — множество всех значений 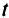 , при которых это решение будет оптимальным. Это множество будет замкнутым интервалом. Надо найти границы интервала. Их находят по формулам
, при которых это решение будет оптимальным. Это множество будет замкнутым интервалом. Надо найти границы интервала. Их находят по формулам
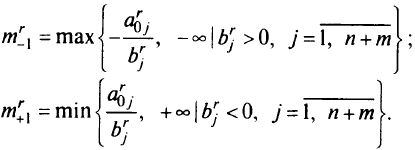
Если нижняя (верхняя) граница данного интервала есть 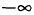
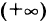 , то найдена нижняя (верхняя) граница области
, то найдена нижняя (верхняя) граница области 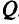 . Для любой границы интервала, такой, что координата ее есть число, по крайней мере один из коэффициентов целевой функции
. Для любой границы интервала, такой, что координата ее есть число, по крайней мере один из коэффициентов целевой функции 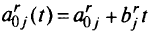 равен нулю. При значениях
равен нулю. При значениях 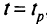 , обращающих выражение
, обращающих выражение 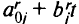 в нуль и называемых критическими, решения задачи определены неоднозначно. Если существует второе базисное решение, то, изменяя базис, можно задавать соседнюю критическую область значений
в нуль и называемых критическими, решения задачи определены неоднозначно. Если существует второе базисное решение, то, изменяя базис, можно задавать соседнюю критическую область значений 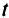 . Если же при попытке заменить базис обнаружена неограниченность решения, то гиперплоскость, соответствующая целевой функции при рассматриваемом ее значении, оказывается параллельной одной из граней выпуклого многогранника, определяемого системой ограничений задачи. Такая грань содержит точки, у которых хотя бы одна из координат будет сколь угодно велика по абсолютному значению. В этом случае достигнута конечная нижняя (верхняя) грань области
. Если же при попытке заменить базис обнаружена неограниченность решения, то гиперплоскость, соответствующая целевой функции при рассматриваемом ее значении, оказывается параллельной одной из граней выпуклого многогранника, определяемого системой ограничений задачи. Такая грань содержит точки, у которых хотя бы одна из координат будет сколь угодно велика по абсолютному значению. В этом случае достигнута конечная нижняя (верхняя) грань области 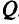 .
.
Пусть при построения обнаружилось, что некоторая точка полученного интервала имеет координату, меньшую (большую), чем координата верхней (нижней) границы интервала, определенного на предыдущем шаге построения. В таком случае говорят, что эта верхняя (нижняя) граница превзойдена. Тогда сама эта верхняя (нижняя) граница является нижней (верхней) границей строящегося интервала. Найдем критическое значение 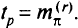 Индекс
Индекс 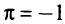 используют при отыскании нижней границы области
используют при отыскании нижней границы области 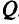 , индекс
, индекс 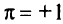 — при отыскании верхней границы. В нашем случае
— при отыскании верхней границы. В нашем случае 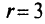 ; отыскиваем нижнюю границу области
; отыскиваем нижнюю границу области 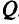 , т.е. полагаем
, т.е. полагаем 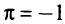 .
.
Положив
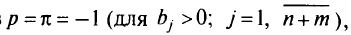
найдем, что
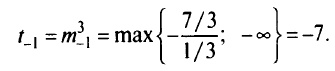
Из табл.5.1 при  следует, что при
следует, что при
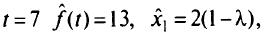
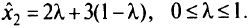
Это критическое значение может быть превзойдено. В табл. 5.1 при 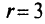 выбран разрешающий элемент, равный 2/3 при
выбран разрешающий элемент, равный 2/3 при 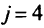 . Общая формула для выбора этой небазисной переменной имеет вид
. Общая формула для выбора этой небазисной переменной имеет вид
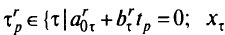
— небазисная переменная}.
Для 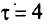 получим следующую таблицу при
получим следующую таблицу при 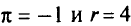 . Она совпадаете таблицей, построенной при
. Она совпадаете таблицей, построенной при 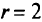 . Так как все
. Так как все 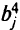 отрицательны, то
отрицательны, то 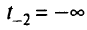 и является нижней границей области
и является нижней границей области  . Из табл. 5.1 при
. Из табл. 5.1 при 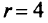 находим, что при
находим, что при
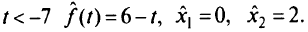
Отыскиваем верхнюю границу области 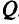 , полагая
, полагая
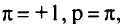
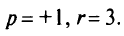
Тогда для
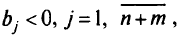
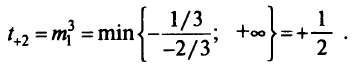
При
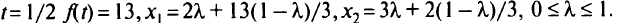
Выбираем разрешающий элемент из столбца для 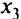 и получаем новую таблицу при
и получаем новую таблицу при 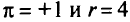 . Из этой таблицы находим новое
. Из этой таблицы находим новое 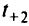 , превышающее критическое значение
, превышающее критическое значение 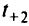 = 1/2. При
= 1/2. При
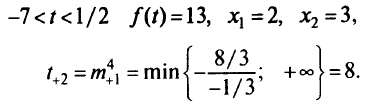
При
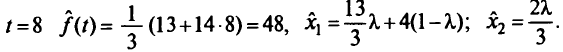
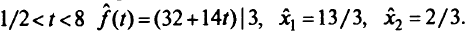
Следующую таблицу строим при 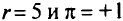 . Получаем
. Получаем 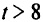 .
.
Окончательные результаты приведены в табл. 5.2 и на рис. 5.1, где показаны «вращение» целевой функции, поведение решающей функции 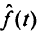 и геометрические образы отношений
и геометрические образы отношений  .
.
Алгоритм решения линейной параметрической задачи в случае зависимости от параметра коэффициентов целевой функции в предположении, что допустимая область, характеризующаяся

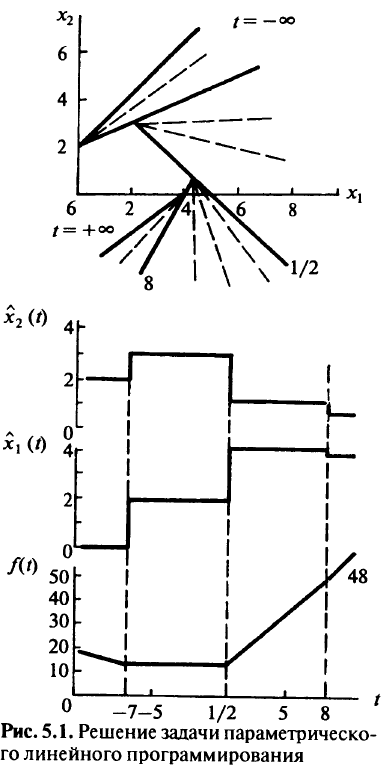
ограничениями задачи, не пуста и что для некоторого значения параметра 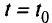 существует оптимальное решение, имеет следующий вид:
существует оптимальное решение, имеет следующий вид:
- При
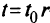 -я симплекс-таблица является оптимальной. Полагаем
-я симплекс-таблица является оптимальной. Полагаем 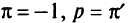 переходим к п. 2.
переходим к п. 2. - Определяем критическое значение
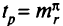
а) если 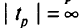 , то достигнута граница области
, то достигнута граница области 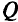
а’) если 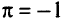 , то отыскиваем нижнюю границу области
, то отыскиваем нижнюю границу области 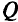 . Полагаем
. Полагаем 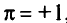 ,
,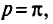 заменяем
заменяем 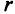 на
на 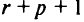 и переходим снова к п. 2;
и переходим снова к п. 2;
а») если 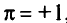 , то отыскиваем верхнюю границу области
, то отыскиваем верхнюю границу области 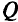 , после чего переходим к п. 3;
, после чего переходим к п. 3;
б) если 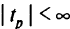 , то определяем возможность превзойти критическое значение выражения для
, то определяем возможность превзойти критическое значение выражения для 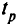 , определяем, иногда подбором из Рис. 5.1. Решение задачи параметрическо-нескольких возможных го линейного программирования значений, новую базисную переменную. В этом случае следует принимать во внимание наличие множества различных решений;
, определяем, иногда подбором из Рис. 5.1. Решение задачи параметрическо-нескольких возможных го линейного программирования значений, новую базисную переменную. В этом случае следует принимать во внимание наличие множества различных решений;
б’) если 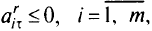 , то достигнута граница области
, то достигнута граница области 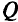 . Переходим к п.
. Переходим к п. 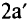 или
или 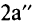 ;
;
б» ) в противном случае строим новую симплекс-таблицу. Заменяя 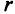 на
на 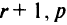 на
на 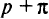 , снова начинаем вычисления с п. 2.
, снова начинаем вычисления с п. 2.
Вычисления прекращаем. Для каждой критической области значение решающей функции 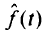 берем из соответствующей таблицы. Там же определены оптимальные значения решающих соотношений
берем из соответствующей таблицы. Там же определены оптимальные значения решающих соотношений 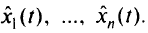
В практических приложениях часто возникают следующие частные случаи параметрической задачи:
1) значение параметра 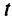 принадлежит некоторому заранее выбранному интервалу
принадлежит некоторому заранее выбранному интервалу 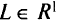 ;
;
2) требуется отыскать только минимум (максимум) функции 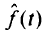 для всех
для всех 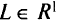 , т.е. требуется определить те значения
, т.е. требуется определить те значения 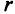 , при которых возможно достижение этого минимума (максимума);
, при которых возможно достижение этого минимума (максимума);
3) требуется отыскать интервал возможных изменений какого-то одного из коэффициентов целевой функции.
Особый интерес представляет задача нахождения наибольшего интервала 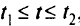 , такого, что оптимальное базисное решение любой из задач, принадлежащих значениям
, такого, что оптимальное базисное решение любой из задач, принадлежащих значениям 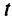 из этого интервала, совпадает с оптимальным базисным решением задачи, принадлежащей значению
из этого интервала, совпадает с оптимальным базисным решением задачи, принадлежащей значению 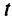 =0.
=0.
Если область определения 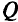 решающей функции
решающей функции 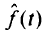 ограничена заранее интервалом
ограничена заранее интервалом 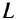 , то вычисления, предписываемые п. 2 алгоритма, заканчивают, когда будут достигнуты границы интервала
, то вычисления, предписываемые п. 2 алгоритма, заканчивают, когда будут достигнуты границы интервала 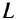 . Если интервал
. Если интервал 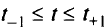 не имеет общих точек с интервалом
не имеет общих точек с интервалом  , то полагают
, то полагают 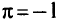 или
или  , в зависимости оттого, будут ли значения
, в зависимости оттого, будут ли значения  меньше или больше.
меньше или больше.
Если в задаче необходимо установить только минимум (максимум) значения решающей функции 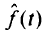 то вычисления, предписываемые п. 2, проводят при
то вычисления, предписываемые п. 2, проводят при 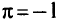 или
или  , в зависимости от того, в каком направлении уменьшается значение функции
, в зависимости от того, в каком направлении уменьшается значение функции 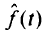 .
.
Если требуется только определить возможность вариации одного из коэффициентов, то сначала устанавливают, существует ли решение при 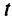 =0, а затем находят это решение. Вводя параметр сводят проблему к определению значений
=0, а затем находят это решение. Вводя параметр сводят проблему к определению значений 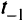 (равных
(равных 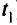 ) и
) и 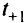 (равных
(равных 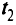 ).
).
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

