Задача об оптимальном распределении самолетов между войсками и учебными полигонами
Рассмотрим задачу о наилучшем распределении выпускаемых промышленностью самолетов между войсками и учебными полигонами, на которых обучаются экипажи для обеспечения лучшей боеготовности противовоздушной обороны.
Пусть некоторая воинская часть, участвующая в боевых вылетах и подготавливающая, кроме того, на своем учебном полигоне экипажи (летчиков), снабжается на протяжении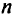 
месяцев самолетами по 
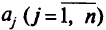единиц в начале каждого месяца. Из них часть 
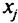, для которой имеются в наличии подготовленные экипажи, направляется сразу в войска, а оставшаяся часть 
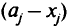— на полигоны для обучения новых экипажей. Боеготовность части определяется числом самолетов с подготовленными экипажами и временем их пребывания в войсках, так называемым числом активных самолето-месяцев.
Возникает задача такого распределения получаемых ежемесячно самолетов между войсками и учебными полигонами, при котором будет достигнута максимальная боеготовность части.
Пусть до начала рассматриваемой программы на полигоне имеется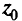 
самолетов. Число самолетов 
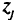используемых на полигоне для обучения в 
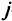-месяце, будет состоять из 
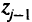самолетов, имевшихся в предыдущем месяце, плюс 
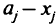самолетов, прибывших в начале 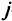-го месяца:
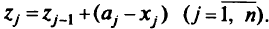
Пусть к началу программы имеется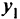 
обученных экипажей, но не обеспеченных самолетами, и в течение месяца на одном самолете обучается к экипажей. Число экипажей обученных к началу 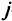-го месяца, будет состоять из числа 
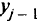, обученных экипажей, имевшихся к началу предыдущего месяца, и числа 
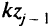экипажей, обученных за 
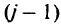-й месяц:
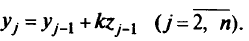
Общее число самолетов, направленных в войска к началу 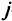-го месяца, не должно превышать обученных к этому моменту экипажей, так что
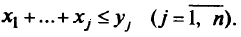
К концу периода, на который рассчитана программа, самолеты, поступившие в войска в первый месяц, обеспечат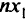 
активных самолето-месяцев. Самолеты, поступившие во второй месяц, обеспечат 
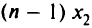активных самолето-месяцев и т.д. Самолеты, поступившие в течение всех месяцев, обеспечат боеготовность в количестве
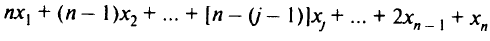
активных самолето-месяцев.
Задача заключается в максимизации
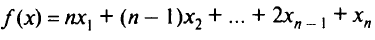
при ограничениях
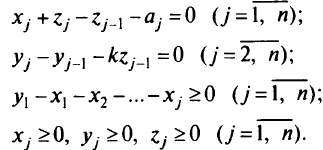
Замечание. К подобной математической модели сводится задача о распределении поступающего в ограниченном количестве сырья (например, металла), часть которого идет на изготовление некоторого изделия, а часть для выпуска оборудования, используемого для производства этого изделия, если конечной целью является максимальный выпуск рассматриваемого изделия.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Задача о закреплении самолетов за воздушными линиями |
| Задача о назначениях (проблема выбора) |
| Задача о рациональном соотношении между различными типами бронебойных снарядов |
| Задачи о покрытии множества |
