Задача о наилучшем использовании посевной площади
Пусть под посев культур отведено 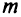 земельных массивов площадью соответственно в
земельных массивов площадью соответственно в 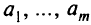 гектаров и пусть средняя урожайность
гектаров и пусть средняя урожайность 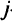 -й культуры на
-й культуры на 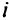 -м массиве составляет
-м массиве составляет 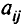 центнеров с гектара, а выручка за один центнер
центнеров с гектара, а выручка за один центнер 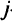 -й культуры составляет
-й культуры составляет 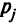 рублей.
рублей.
Определить, какую площадь на каждом массиве следует отвести под каждую из культур, чтобы получить максимальную выручку, если по плану должно быть собрано не менее 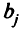 центнеров
центнеров 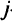 -й
-й 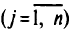 культуры.
культуры.
Обозначим через 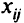 площадь, которую предполагается отвести под
площадь, которую предполагается отвести под 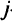 -ю культуру на
-ю культуру на 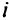 -м массиве, так что
-м массиве, так что
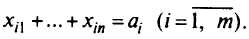
Ожидаемый средний урожай 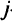 -й культуры со всех массивов
-й культуры со всех массивов
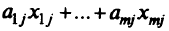
по плану должен быть не менее 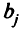 центнеров:
центнеров:
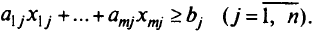
Ожидаемая выручка за урожай 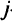 -й культуры
-й культуры
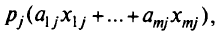
а за урожай всех культур
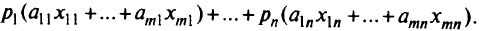
Таким образом, задача заключается в максимизации
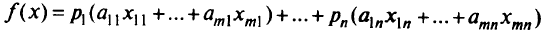
от 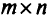 переменных
переменных
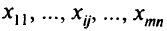
при выполнении следующих ограничений:
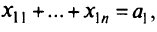
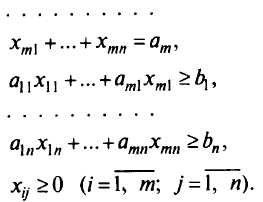
Как обычно, задачу решают симплекс-методом.
Иногда задача об оптимальном распределении посевной площади выглядит так: имеющуюся посевную площадь распределить под посев культур таким образом, чтобы обеспечить максимальный урожай при соблюдении определенного соотношения 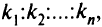 в котором должны производиться эти культуры.
в котором должны производиться эти культуры.
Введением дополнительной переменной 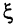 такой, что
такой, что
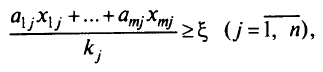
рассматриваемая задача сводится к задаче линейного программирования — максимизировать
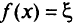
при ограничениях
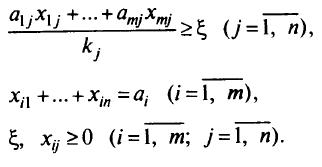
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

