Постановка задачи об оптимальном раскрое материалов (о минимизации отходов)
Пусть некоторый полуфабрикат (например, листы фанеры) поступил на предприятие в виде 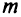 различных партий, содержащих соответственно
различных партий, содержащих соответственно 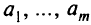 единиц полуфабриката одинакового для каждой партии размера. Из поступивших полуфабрикатов требуется изготовить возможно большее число комплектов деталей, в каждый из которых входит
единиц полуфабриката одинакового для каждой партии размера. Из поступивших полуфабрикатов требуется изготовить возможно большее число комплектов деталей, в каждый из которых входит 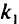 деталей первого вида,
деталей первого вида, 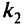 деталей второго вида, …,
деталей второго вида, …, 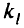 деталей
деталей 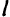 вида. Пусть каждую единицу полуфабриката можно раскроить на детали различными способами, причем при раскрое единицы
вида. Пусть каждую единицу полуфабриката можно раскроить на детали различными способами, причем при раскрое единицы 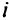 -й партии
-й партии 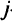 -м способом получается
-м способом получается 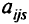 деталей
деталей 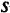 -го вида.
-го вида.
Обозначим через 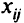 число единиц из
число единиц из 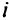 -й партии полуфабрикатов, которые намечено раскроить
-й партии полуфабрикатов, которые намечено раскроить 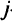 -м способом, так что из
-м способом, так что из 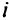 -й партии при
-й партии при 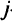 -м способе раскроя будет получено
-м способе раскроя будет получено 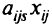 деталей
деталей 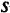 -го вида. Всего же по плану из всей
-го вида. Всего же по плану из всей 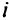 -й партии деталей
-й партии деталей 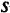 -го вида будет получено
-го вида будет получено
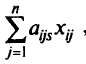
а из всех 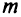 партий их будет получено
партий их будет получено
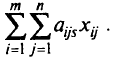
как в каждый комплект готовой продукции должно входить 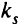 деталей
деталей 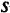 -го вида, то
-го вида, то
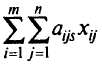
деталей позволит их использовать
для составления
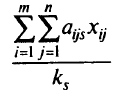
комплектов, и, таким образом, число полных комплектов, которое можно будет выпустить по данному плану 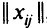 , равно наименьшему из частных
, равно наименьшему из частных
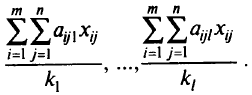
Введением дополнительной переменной 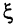 сведем рассматриваемую задачу к задаче максимизации
сведем рассматриваемую задачу к задаче максимизации 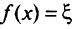 при ограничениях
при ограничениях
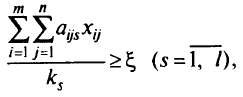
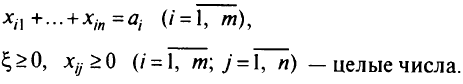
Не всегда эту задачу решают как целочисленную. Если значения переменных в полученном оптимальном решении задачи линейного программирования достаточно велики, то приближенное целочисленное решение получают из него путем округления до ближайших допустимых целых чисел.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

