Задача о перевозках с перегрузкой
Забежав несколько вперед (см. гл. 3), укажем, что сетевой подход позволяет использовать алгоритм транспортной задачи для решения более сложных задач. Втранспортной задаче предполагается, что ни в одном из маршрутов, соединяющих источник с некоторым стоком, другие источники и стоки не могут быть использованы в качестве промежуточных пунктов. Если считать допустимой перевозку фузов из источника в сток через другие источники и стоки, то новая задача может быть сведена к обычной транспортной задаче. Объем вычислений, естественно, возрастает, так как в сеть будут включены дополнительные маршруты, соединяющие каждый источник со всеми другими источниками и каждый сток со всеми другими стоками. Считаем, что транспортные затраты с^, соответствующие дополнительным маршрутам, известны. Новая задача сводится к модифицированной транспортной задаче, в которой предложения и спрос, соответствующие дополнительным маршрутам, заданы таким образом, что они не влияют на выбор маршрутов, осуществляемый в основном алгоритме. Выполнение последнего требования необходимо, поскольку ограничения на поток по дополнительным маршрутам, задаваемые предложением и спросом, являются фиктивными и вводятся только для вычислительных целей.
Пусть 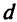 — минимальная из величин
— минимальная из величин 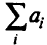 и
и 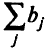 — суммарных предложения и спроса, т.е.
— суммарных предложения и спроса, т.е. 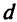 — это реальный поток, протекающий по модифицированной сети. Тогда очевидно, что величину спроса
— это реальный поток, протекающий по модифицированной сети. Тогда очевидно, что величину спроса 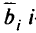 -го исходного источника и величину предложения
-го исходного источника и величину предложения 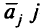 -го исходного стока можно принять равными
-го исходного стока можно принять равными 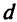 , т.е. весь поток может протекать через один источник или через один сток. Поскольку
, т.е. весь поток может протекать через один источник или через один сток. Поскольку  то исходные величины предложения и спроса должны быть увеличены на
то исходные величины предложения и спроса должны быть увеличены на 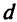 . Если же увеличить исходные данные на
. Если же увеличить исходные данные на 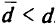 , то некоторые планы перевозок, допустимые в исходной задаче, в модифицированной задаче станут недопустимыми. Выбор
, то некоторые планы перевозок, допустимые в исходной задаче, в модифицированной задаче станут недопустимыми. Выбор 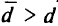 не скажется на решении задачи. Поэтому выбирают
не скажется на решении задачи. Поэтому выбирают 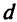 .
.
Рассмотрим традиционную транспортную задачу (табл. 2.12).
Пусть в ней каждый источник и каждый сток может использоваться в качестве промежуточного пункта (узла). Здесь 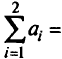
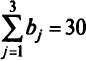 следовательно, в модифицированной задаче надо выбрать
следовательно, в модифицированной задаче надо выбрать 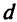 = 30.
= 30.

Новая задача о перевозках может быть сведена к транспортной задаче со следующими величинами предложения и спроса для стоков и источников:

Матрица условий модифицированной транспортной задачи для решения задачи перевозок с перегрузкой приведена в табл. 2.13. Транспортные затраты 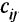 для дополнительных маршрутов (три последние строки и два последних столбца в табл. 2.13) предполагаются известными.
для дополнительных маршрутов (три последние строки и два последних столбца в табл. 2.13) предполагаются известными.
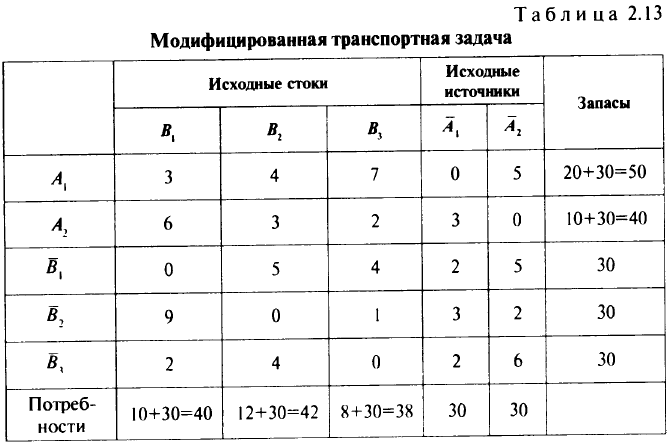
Эту задачу можно решить методом потенциалов. Решив модифицированную транспортную задачу, тем самым решим поставленную задачу о перевозках.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

