Двойственность в задачах линейного программирования
В разд. 1.6 было показано, что в ряде случаев проще решить двойственную задачу математического программирования, чем прямую. Рассмотрим теорию двойственности для задач линейного программирования. Для каждой такой задачи можно построить другую задачу, называемую двойственной. Понятие двойственности дает ощутимые преимущества при построении алгоритмов решения задач линейного программирования. Запишем обе задачи:
Симметричность обеих задач очевидна. Неравенству в одной задаче соответствует неотрицательная переменная другой. Равенству одной задачи соответствует свободная переменная другой. Задача, двойственная к двойственной задаче, есть исходная (прямая) задача. Таким образом, любую из этой пары задач можно считать прямой.
Для стандартного и канонического видов задачи линейного программирования двойственные задачи можно записать следующим образом.
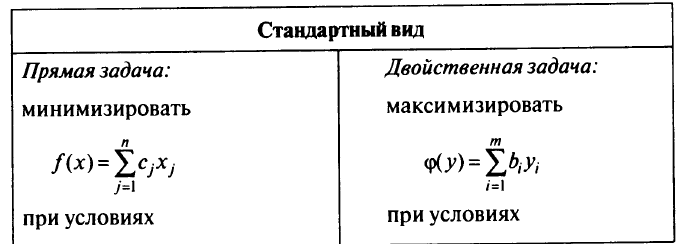
Из сравнения обеих задач нетрудно видеть, что:
1) матрицу из коэффициентов при переменных в исходной задаче
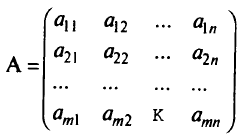
и аналогичную матрицу в двойственной задаче
получают друг из друга простой заменой строк столбцами с сохранением их порядка (такую операцию называют транспонированием и обозначают значком «т»);
2) в исходной задаче имеется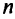 
переменных и 
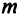ограничений, в двойственной — 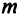переменных и 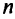ограничений;
3) в правых частях систем ограничений каждой из задач стоят коэффициенты целевой функции, взятой из другой задачи;
4) в исходной задаче в систему ограничений входят неравенства типа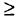 
и требуется минимизировать целевую функцию 
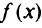, в двойственной задаче в систему ограничений входят неравенства типа 
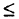и требуется максимизировать целевую функцию 
.
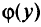В теории двойственности доказывают следующую теорему: пусть дана пара двойственных задач линейного программирования (заданных в стандартном виде). Тогда справедливо одно и только одно из следующих утверждений:
- Обе задачи имеют оптимальные решения и оптимальные значения целевых функций равны, т.е.
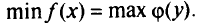. - Одна из задач не имеет ни одного допустимого решения, а другая имеет по крайней мере одно допустимое решение, но не имеет оптимального решения (целевая функция на множестве допустимых решений неограничена).
- Ни одна пара задач не имеет допустимых решений.
Между решениями пары двойственных задач линейного программирования существуют и другие соотношения, которые устанавливаются теоремами о дополняющей нежесткости: для того чтобы допустимые решения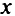 
и 
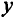прямой и двойственной задач были оптимальными, необходимо и достаточно, чтобы выполнялись следующие соотношения:
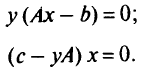
Условие(а)равносильно условиям:
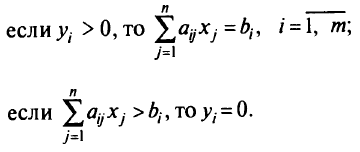
Условие(б)равносильно условиям:
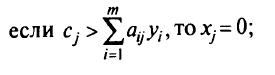
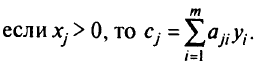
Это условия дополняющей нежесткости в слабой форме. В сильной форме условия дополняющей нежесткости утверждают, что:
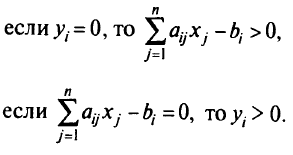
Может случиться, что
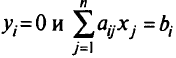
одновременно. Новсегда существует по крайней мере одна пара оптимальных решений, для которых условия
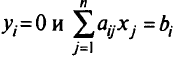
не могут выполняться одновременно.
Нетрудно проверить, что, если вектор 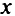— решение прямой задачи, а вектор 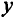— решение двойственной задачи, то сумма произведений соответствующих координат векторов 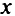и 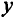равна нулю (скалярное произведение векторов 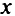и 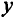равно нулю).
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
