Симплекс-метод — основной метод решения задач линейного программирования
Рассмотрим задачу линейного программирования в канонической форме:
найти минимум функции
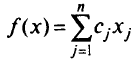
при условиях
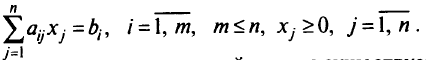
Предполагается, что решение этой задачи существует. Для его нахождения надо сначала найти допустимые базисные решения, а затем из них выбрать оптимальное. Для этого поочередно из столбцов матрицы
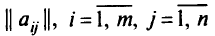
выбираем 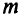 столбцов и решаем систему из
столбцов и решаем систему из 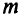 уравнений с
уравнений с 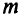 неизвестными. Такой метод требует решения
неизвестными. Такой метод требует решения
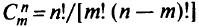
систем уравнений, что практически невозможно даже при небольших значениях 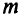 .
.
В 1949 г. американский математик Дж. Данциг разработал симплекс-метод, ставший основным для решения задач линейного программирования. Разберем главные моменты этого метода на небольшом числовом примере:
минимизировать
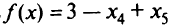
при ограничениях:
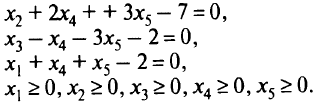
Определитель, составленный из коэффициентов при неизвестных
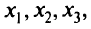
имеет вид
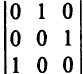
и не равен нулю. Поэтому ранг матрицы ограничений равен 3, базисные переменные — 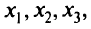 , а свободные переменные —
, а свободные переменные — 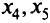 . Выразим базисные переменные через свободные:
. Выразим базисные переменные через свободные:
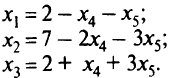
Базисное решение (при нулевых значениях свободных переменных 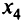 и
и 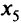 ) в данном случае имеет вид
) в данном случае имеет вид
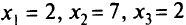
и является допустимым (значения 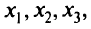 положительны). Целевая функция при таких значениях переменных
положительны). Целевая функция при таких значениях переменных 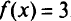 . Но ее значение может быть уменьшено, если увеличить значение переменной
. Но ее значение может быть уменьшено, если увеличить значение переменной 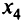 , входящей с отрицательным коэффициентом. Очевидно, что увеличивать
, входящей с отрицательным коэффициентом. Очевидно, что увеличивать 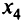 можно до тех пор, пока не будут нарушены условия-ограничения задачи, в частности, пока переменные
можно до тех пор, пока не будут нарушены условия-ограничения задачи, в частности, пока переменные 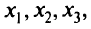 будут неотрицательны. Например, если
будут неотрицательны. Например, если
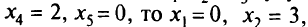
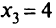
новое допустимое решение. При 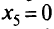 переменная
переменная 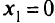 ,
,
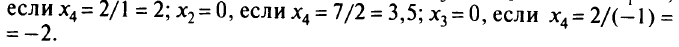
Чтобы ни одна из переменных 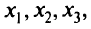 не стала отрицательной, надо выбрать наименьшее положительное отношение элементов столбца свободных членов к соответствующим коэффициентам при
не стала отрицательной, надо выбрать наименьшее положительное отношение элементов столбца свободных членов к соответствующим коэффициентам при 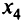 . Берем
. Берем 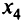 = 2, тогда
= 2, тогда 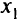 будет равна нулю, т.е.
будет равна нулю, т.е. 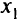 переводим в свободные переменные, а
переводим в свободные переменные, а 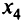 = 2 становится базисной переменной. Ограничения и целевую функцию надо выразить теперь через
= 2 становится базисной переменной. Ограничения и целевую функцию надо выразить теперь через 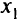 и
и 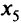 : из первого уравнения имеем
: из первого уравнения имеем
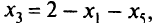
из второго
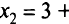
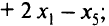
из третьего
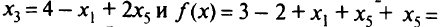
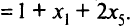
В данном случае любое увеличение значений свободных переменных 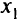 и
и 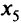 ведет к увеличению (но не к уменьшению) значений целевой функции, т.е. получено оптимальное решение:
ведет к увеличению (но не к уменьшению) значений целевой функции, т.е. получено оптимальное решение:
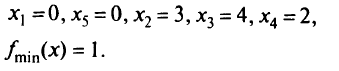
Какие выводы можно сделать из этого примера? Во-первых, нужно так разделить базисные и свободные переменные, чтобы получить допустимое базисное решение, а затем выразить базисные переменные и целевую функцию через свободные переменные. Во-вторых, по знаку коэффициентов при неизвестных в целевой функции следует определить: а) не достигли ли мы уже оптимального решения (нет отрицательных коэффициентов); б) значение какой переменной лучше увеличить, т.е. какую переменную надо перевести в свободные. Другими словами, определяя минимальное положительное отношение элементов столбца свободных членов к коэффициентам при новой свободной переменной, находим переменную, которую необходимо перевести из базисных в свободные. После этого выражаем условия-ограничения и целевую функцию через новые свободные переменные.
Процесс повторяют до тех пор, пока не будет получено оптимальное решение. Если среди коэффициентов при неизвестных в целевой функции есть положительный, а все коэффициенты в условиях-ограничениях при нем неположительны, то задача линейного программирования не имеет оптимального решения, минимальное значение целевой функции равно —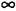 .
.
Рассмотрим геометрическуюинтерпретациюсимплекс-метода, давшую название методу.
В условия одной из первых задач линейного программирования, для которых Данциг разработал вычислительный метод, входили ограничения вида
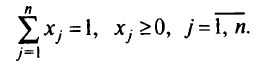
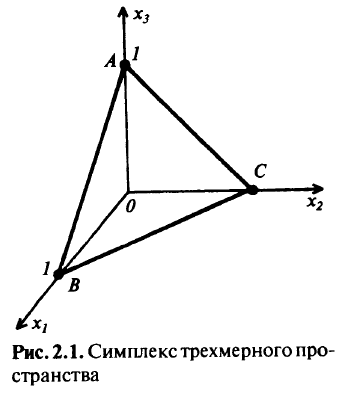
Эти ограничения в 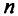 -мерном пространстве определяют симплекс. Симплекс трехмерного пространства изображен на рис. 2.1. Рассмотрим неравенство
-мерном пространстве определяют симплекс. Симплекс трехмерного пространства изображен на рис. 2.1. Рассмотрим неравенство 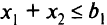 при условиях
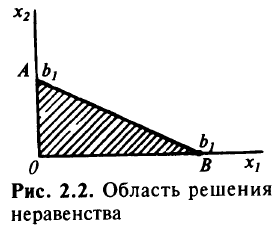
при условиях 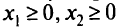 . Область решения этого неравенства показана на рис. 2.2. Данное неравенство можно преобразовать в уравнение введением слабой переменной
. Область решения этого неравенства показана на рис. 2.2. Данное неравенство можно преобразовать в уравнение введением слабой переменной 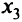 . Тогда получим систему
. Тогда получим систему
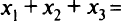
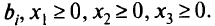
Областью решений этой системы является треугольник 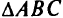 , показанный на рис. 2.1, если принять, что
, показанный на рис. 2.1, если принять, что 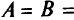
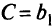 Каждой точке треугольной области рис. 2.1 соответствует точка области на рис. 2.2. Соответствие можно устанавливать, проектируя эту треугольную область на плоскость
Каждой точке треугольной области рис. 2.1 соответствует точка области на рис. 2.2. Соответствие можно устанавливать, проектируя эту треугольную область на плоскость 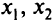 . Если придать слабой переменной
. Если придать слабой переменной 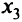 постоянное значение
постоянное значение 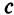 , то
, то 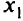 и
и 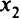 должны удовлетворять уравнению неравенства
должны удовлетворять уравнению неравенства 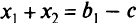 , которое является уравнением прямой, параллельной
, которое является уравнением прямой, параллельной 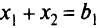 . Если слабая переменная равна нулю, те
. Если слабая переменная равна нулю, те 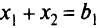 Таким образом, значение слабой переменной может служить мерой близости точки из треугольной области к границе
Таким образом, значение слабой переменной может служить мерой близости точки из треугольной области к границе 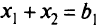 полупространства, определяемого исходным неравенством.
полупространства, определяемого исходным неравенством.
В общем случае в симплекс-методе процедуру поиска начинают с допустимой вершины, а затем переходят в соседнюю вершину так, чтобы значение целевой функции «улучшилось». В пространстве векторов свободных переменных возрастание значения одной из свободных переменных от нуля, при котором остальные свободные переменные остаются равными нулю, соответствует движению из начала системы координат, образованной свободными переменными, по одной из координатных осей. При этом поскольку 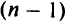 свободных переменных равны нулю,
свободных переменных равны нулю, 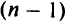 ограничений задачи выполняются как равенства. Другими словами, все соседние с началом координат вершины (которые соответствуют текущему решению) связаны с началом координат
ограничений задачи выполняются как равенства. Другими словами, все соседние с началом координат вершины (которые соответствуют текущему решению) связаны с началом координат 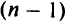 ребрами выпуклого многогранника.
ребрами выпуклого многогранника.
Возрастание от нуля значения некоторой свободной переменной может привести к тому, что эта переменная станет базисной. Для того чтобы получить в качестве решения вершину, необходимо заменить одну из базисных переменных на свободную, т.е. произвести соответствующее перемещение вдоль одной из координатных осей до тех пор, пока не будет достигнута другая вершина. Если двигаться дальше, то будет нарушено условие неотрицательности переменных.
Таким образом, в симплекс-методе начинают с локальной координатной системы, начало координат которой соответствует текущему решению, и перемещаются вдоль ребра к соседней вершине, в которой значение целевой функции «улучшается». После перехода в новую вершину рассматривают новую систему координате началом в этой вершине. Если движение осуществляют согласно критерию (выбирают минимальный отрицательный коэффициент при неизвестных в целевой функции), то это соответствует спуску по самому крутому ребру из всех пересекающихся в начале координат. Величину изменения целевой функции за одну итерацию определяют как углом наклона (крутизной) ребра, так и длиной ребра. Более точно она равна минимальному значению по 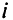 величины
величины 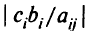 для данного
для данного 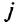 , где
, где 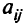 — соответствующий элемент вектора-столбца
— соответствующий элемент вектора-столбца 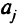 для
для 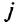 -й свободной переменной.
-й свободной переменной.
Итак, в симплекс-методе всегда считают, что в первую таблицу внесено допустимое базисное решение. В задачах, описывающих реальные системы, допустимое базисное решение подобрать трудно. Для этого решают вспомогательную задачу линейного программирования, которая позволяет не только найти допустимое базисное решение, но и установить, совместна ли система ограничений исходной задачи.
Пусть система ограничений исходной задачи записана в следующем виде:
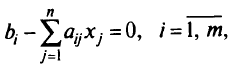
где 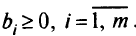 Этого нетрудно добиться, умножив при необходимости уравнения на -1. Введем новые переменные
Этого нетрудно добиться, умножив при необходимости уравнения на -1. Введем новые переменные
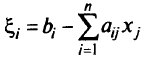
и рассмотрим новую целевую функцию
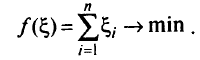
Допустимое решение для задачи (а), (б) сразу задано решения задачи возможны следующие случаи:
1) 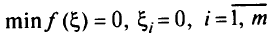 (все
(все 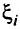 стали свободными переменными)—полученное решение
стали свободными переменными)—полученное решение 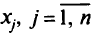 , является допустимым решением исходной задачи линейного программирования;
, является допустимым решением исходной задачи линейного программирования;
2) 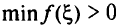 — система ограничений исходной задачи несовместна.
— система ограничений исходной задачи несовместна.
В первом случае можно отметить две особенности:
- Целевая функция
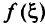 достигла своего минимума, равного нулю, а некоторые из переменных
достигла своего минимума, равного нулю, а некоторые из переменных 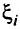 находятся среди базисных, хотя и равны нулю. При этом нет необходимости обращать внимание на знаки в строке для целевой функции (можно любую свободную переменную выводить в базисные), так как значение целевой функции не изменится, но следует выполнить условия, обеспечивающие допустимость нового базисного решения (рассмотреть минимальное положительное отношение).
находятся среди базисных, хотя и равны нулю. При этом нет необходимости обращать внимание на знаки в строке для целевой функции (можно любую свободную переменную выводить в базисные), так как значение целевой функции не изменится, но следует выполнить условия, обеспечивающие допустимость нового базисного решения (рассмотреть минимальное положительное отношение). - Даже после выполнения предыдущего пункта в строке для базисной переменной
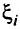 нет положительных элементов (нельзя получить положительное отношение). Это означает, что переменные, входящие в уравнение для
нет положительных элементов (нельзя получить положительное отношение). Это означает, что переменные, входящие в уравнение для 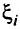 с ненулевыми коэффициентами, должны быть равными нулю в данной задаче. В процессе дальнейшего решения их надо исключить из рассмотрения.
с ненулевыми коэффициентами, должны быть равными нулю в данной задаче. В процессе дальнейшего решения их надо исключить из рассмотрения.
Наряду с решением вспомогательной задачи линейного программирования (а), (б) преобразуется и целевая функция исходной задачи, которая приписывается в задаче (а), (б) в виде дополнительной строки.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

