Дифференциальные зависимости при прямом поперечном изгибе
Построение эпюр поперечных сил и изгибающих моментов существенно упрощается при использовании дифференциальных зависимостей между изгибающим моментом, поперечной силой и интенсивностью равномерно распределенной нагрузки (теорема Журав-ского):
Поперечная сила равна производной от изгибающего моменты по длине балки:
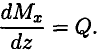
Интенсивность равномерно распределенной нагрузки равна производной от поперечной силы по длине балки:
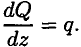
Из выше указанного следует:
если
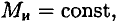
то
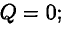
если
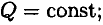
то
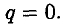
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
| Внутренние силовые факторы при изгибе |
| Знаки поперечных сил и изгибающих моментов |
| Деформации при чистом изгибе |
| Формула для расчета нормальных напряжений при изгибе |
