Работа постоянной силы на криволинейном пути
Пусть точка 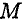 движется по дуге окружности и сила
движется по дуге окружности и сила 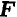 составляет некоторый угол
составляет некоторый угол 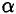 с касательной к окружности (рис. 15.5).
с касательной к окружности (рис. 15.5).
Вектор силы можно разложить на две составляющие:
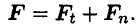
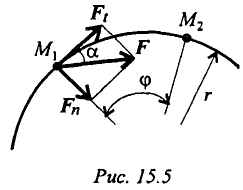
Используя принцип независимости действия сил, определим работу каждой из составляющих силы отдельно:

где 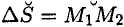 — пройденный путь.
— пройденный путь.
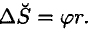
Нормальная составляющая силы  всегда направлена перпендикулярно перемещению и, следовательно, работы не производит:
всегда направлена перпендикулярно перемещению и, следовательно, работы не производит: 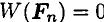 .
.
При перемещении по дуге обе составляющие силы разворачиваются вместе с точкой 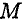 . Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением.
. Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением.
Будем иметь: 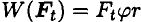 .
.
Касательную силу 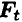 обычно называют окружной силой.
обычно называют окружной силой.
Работа при криволинейном пути — это работа окружной силы:
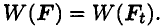
Произведение окружной силы на радиус называют вращающим моментом:
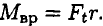
Работа силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота:
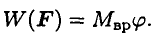
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
| Принцип кинетостатики (принцип Даламбера) |
| Работа силы |
| Работа силы тяжести |
| Работа равнодействующей силы |

