Развертка кругового конуса

Развертка кругового конуса

На рис. 9.6 показан пример построения развертки боковой поверхности прямого кругового конуса со срезом фронтально-проецирующей плоскостью 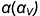, которая пересекает его поверхность по эллипсу.

Построение развертки боковой поверхности конуса выполняется по алгоритму, приведенному выше для построения развертки пирамиды, с некоторыми дополнениями.

Развертка выполняется по предлагаемому алгоритму

1-е действие. Заменить прямой круговой конус вписанной правильной 12-угольной пирамидой с ребрами-образующими.

2-е действие. Построить развертку боковой поверхности пирамиды по натуральным величинам ребер (образующих) и сторон основания, выполнив следующие графические действия:

2.1. Отметить на свободном поле чертежа точку 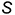и провести дугу радиусом 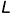, равным натуральной величине всех образующих конуса (ребер пирамиды).

2.2. Отметить на дуге точку 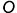на вертикальной линии симметрии развертки и построить вправо и влево на дуге засечками, равными сторонам-хордам 12-угольника, точки, соответствующие вершинам этого многоугольника; пронумеровать эти точки и соединить их с вершиной развертки, построив таким образом вспомогательные ребра-образующие (грани пирамиды).

3-е действие. Достроить на развертке линию среза конуса фронтально-проецирующей плоскостью 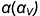, выполнив следующие графические действия:

3.1. На фронтальной проекции конуса перенести горизонтально на натуральную величину образующей 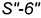точки сечения, отмеченные на вспомогательных образующих, то есть вращением вокруг оси 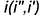построить натуральные величины отрезков образующих-ребер сечения.

3.2. Отложить на соответствующих образующих развертки натуральные величины отрезков образующих-ребер до точек сечения (отмечены на фронтальной проекции и на развертке фигурными скобками отрезки 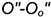образующей для точки и 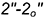образующей для точки ) и соединить построенные точки сечения на развертке плавной кривой линией.

4-е действие. Оформить чертеж развертки, проведя сплошными толстыми линиями контур построенной развертки.

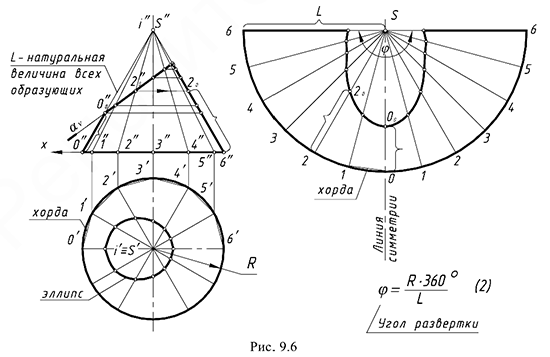
Для построения более точной развертки следует вычислить по формуле (2) (рис. 9.6, где — радиус основания конуса; — длина образующей конуса) угол развертки и разделить дугу развертки на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.

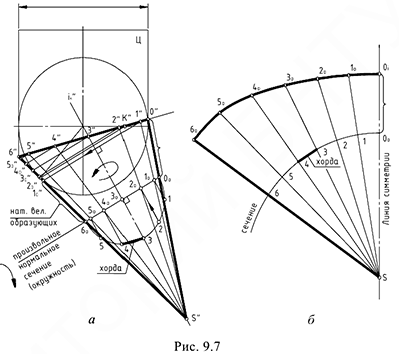
На рис. 9.7, а дан чертеж поверхностей кругового цилиндра и кругового конуса, описанных вокруг сферы, и построена линия пересечения этих поверхностей по теореме Г. Монжа. На рис. 9.7, б построена развертка конической части этой конструкции по следующему графическому алгоритму:

1-е действие. Провести произвольное сечение, перпендикулярное оси конуса, и повернуть половину окружности сечения в очерковую плоскость конуса.

2-е действие. Разделить окружность сечения на 6 частей и перенести точки 1-6 параллельно оси конуса на линию сечения (проекцию окружности). то есть построить точки .

3-е действие. Через вершину конуса 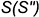и точки 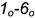провести образующие конуса до пересечения с проекцией линии пересечения с проекцией линии пересечения цилиндра и конуса .

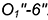4-е действие. Вращением построенных образующих вокруг оси конуса перенести точки 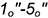на очерковую образующую 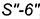, имеющую на чертеже натуральную величину.

5-е действие. На свободном поле чертежа провести радиусом 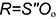дугу и отложить на этой дуге шесть отрезков-хорд, на которые было поделено сечение конуса.

6-е действие. Через точку 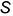на развертке и построенные точки 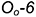провести семейство образующих.

1-е действие. Отложить от точек 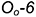на каждой образующей развертки соответствующие натуральные величины образующих, взятые с чертежа, то есть отрезки 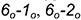и т. д.

8-е действие. Построенные на концах семейства образующих точки соединить плавной кривой и оформить чертеж развертки (построена половина развертки).

На рис. 9.8 показано построение развертки боковой поверхности боковой поверхности усеченного конуса (если вершину конуса на чертеже достроить нельзя) с основаниями, равным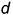и и .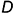

Предварительно на чертеже усеченного конуса строится вспомогательный неусеченный конус подобный заданному так, чтобы отношение диаметра 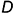исходного конуса к диаметру вспомогательного конуса 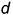, было целым число, то есть 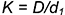— целое число, где 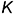— коэффициент кратности оснований конусов.

Примем 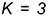и впишем в заданный конус вспомогательный конус с вершиной .

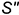Достроим горизонтальную проекцию вспомогательного конуса и разделим половину окружности основания 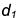на 6 частей (1-6).

Далее приступаем к построению развертки половины усеченного конуса по следующему графическому алгоритму:

1-е действие. На свободном поле чертежа построить развертку вспомогательного конуса с вершиной 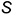(см. рис. 9.8), то есть построить точки 0-2-4-6 на дуге развертки.

2-е действие. На оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку 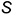и провести семейство лучей, соединяющих соответственно произвольную точку 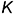с точками 0-2-4-6 развертки вспомогательного конуса.

3-е действие. Отложить на проведенных лучах отрезки, величины которых определяются произведениями:

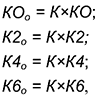
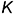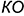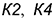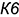где — принятый коэффициент пропорциональности, а величины , и следует измерить на строящейся развертке.

На концах лучей определяются точк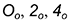и и .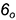

4-е действие. Через построенные точки на концах лучей провести прямые 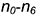, каждая из которых должна быть соответственно параллельна образующим вспомогательного конуса на его развертке.

5-е действие. На проведенных прямых 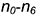отложить натуральную величину длин образующих заданного усеченного конуса .

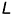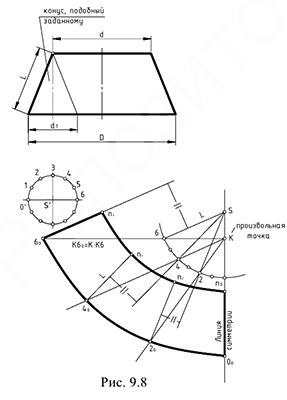
6-е действие. Оформить чертеж развертки, соединив построенные точки развертки лекальными прямыми.

Условные развертки поверхностей

Условные развертки можно выполнить для некоторых неразвертыва-ющихся поверхностей.

Рассмотрим построение условных разверток неразвертывающихся поверхностей сферы и открытого тора (кругового кольца).

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

 Начертательная геометрия для 1 курса

Возможно эти страницы вам будут полезны:

Развертка поверхности геодезической линии

Развертка кругового цилиндра

Развертка поверхности открытого тора

Развертка сферической поверхности