Построение проекций точек, лежащих на поверхности пирамиды
На рис. 7.2 показан пример построения горизонтальных и профильных проекций точек 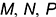 и
и 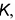 лежащих на поверхности пирамиды и заданных фронтальными проекциями
лежащих на поверхности пирамиды и заданных фронтальными проекциями 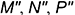 и
и 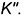
- Построение горизонтальных проекций точек, лежащих на поверхности пирамиды:
- горизонтальная проекция
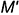 точки
точки 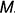 , лежащей на ребре пирамиды
, лежащей на ребре пирамиды  , определяется на горизонтальной проекции
, определяется на горизонтальной проекции 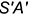 этого ребра;
этого ребра; - горизонтальные проекции точек
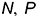 и
и 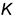 построены на вспомогательных прямых, проведенных через их заданные фронтальные проекции
построены на вспомогательных прямых, проведенных через их заданные фронтальные проекции 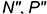 и
и 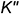 параллельно основанию пирамиды.
параллельно основанию пирамиды.
Рассмотрим графический алгоритм для построения горизонтальных проекций точек, лежащих на гранях пирамиды (на примере заданной точки 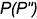 ), действия которого определяются теоремами о принадлежности точки и прямой плоскости.
), действия которого определяются теоремами о принадлежности точки и прямой плоскости.
Графический алгоритм:
1-е действие. Провести через точку 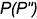 на поверхности пирамиды вспомогательную линию
на поверхности пирамиды вспомогательную линию 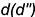 , параллельную основанию пирамиды, которая пересекает ребро
, параллельную основанию пирамиды, которая пересекает ребро 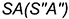 по вспомогательной точке
по вспомогательной точке 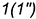 .
.
2-е действие. Построить горизонтальную проекцию точки 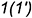 по ее принадлежности ребру
по ее принадлежности ребру 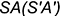 .
.
3-е действие. Через построенную точку 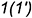 провести горизонтальную проекцию
провести горизонтальную проекцию 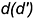 вспомогательной линии параллельно стороне
вспомогательной линии параллельно стороне 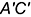 основания пирамиды.
основания пирамиды.
4-е действие. Построить по линии связи горизонтальную проекцию 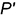 точки
точки  по ее принадлежности вспомогательной линии
по ее принадлежности вспомогательной линии 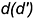 .
.
Повторить действия графического алгоритма и построить аналогично горизонтальные проекции 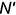 и
и 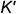 точек
точек 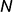 и
и 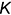 .
.
Проекции точек на поверхности пирамиды можно строить также с помощью вспомогательных прямых, проходящих через ее вершину. Смотри построение проекции точки 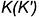 с помощью вспомогательной прямой
с помощью вспомогательной прямой 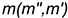 (рис. 7.2).
(рис. 7.2).
Построение профильных проекций точек, лежащих на поверхности пирамиды:
- профильные проекции заданных точек
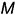 и
и 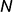 построены по их принадлежности ребрам пирамиды:
построены по их принадлежности ребрам пирамиды: 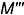 — по принадлежности ребру
— по принадлежности ребру 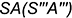 ;
;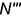 — по принадлежности ребру
— по принадлежности ребру 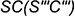 ;
;- профильные проекции точек
 и
и 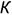 построены по координатам
построены по координатам 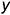 :
:  — определяется координатой
— определяется координатой 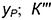 — определяется координатой
— определяется координатой 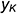 (на профильной проекции
(на профильной проекции 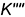 невидима, так как лежит на невидимой грани
невидима, так как лежит на невидимой грани  (взята в скобки).
(взята в скобки).
!!! Запомните характерные признаки очерков пирамиды на чертеже -два треугольника и многоугольник основания. Для усеченной пирамиды — две трапеции и многоугольник основания!
Построение проекций призмы и пирамиды со срезами плоскостями частного положения
Любая плоскость пересекает поверхность призмы и пирамиды по замкнутым ломаным линиям, вершины которых лежат в точках пересечения ребер, граней и оснований многогранника с плоскостями срезов.
Следовательно, построение срезов на проекциях гранных поверхностей сводится к построению проекций точек, лежащих на поверхности призмы или пирамиды.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Построение проекций прямой правильной призмы |
| Построение проекций правильной пирамиды |
| Построение проекций призмы со срезами плоскостями частного положения |
| Поверхности вращения |

