Способ вращения вокруг прямой уровня — горизонтальной или фронтальной прямой
Сущность способа в том, что плоскость общего положения изменяет свое положение в пространстве относительно плоскостей проекций вращением вокруг линии уровня до положения, параллельного плоскости проекций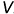 
(или 
).
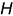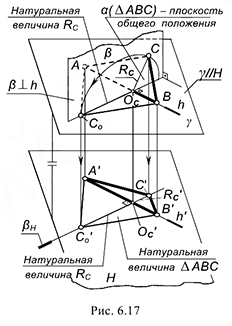
На рис. 6.17 показана наглядная картина вращения плоскости общего положения 
вокруг горизонтальной прямой. Пусть сторона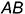 
треугольника 
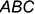лежит в плоскости 
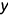, параллельной плоскости проекций 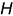, и является горизонтальной прямой 
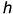, вокруг которой и будет повернута плоскость .
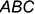Поскольку вершины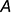 
и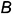 
треугольника лежат на оси вращения 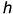и, следовательно, неподвижны, то требуется повернуть вокруг прямой уровня 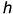только вершину 
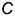так, чтобы она совместилась с плоскостью 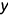. Вершина 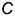вращается вокруг горизонтальной прямой 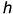(стороны 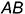) в плоскости 
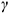, перпендикулярной оси вращения .
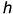После поворота треугольник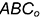 
лежит в плоскости 
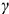и, следовательно, параллелен плоскости 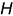. Точка 
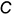имеет радиус вращения 
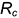и на плоскость 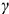этот радиус проецируется в натуральную величину.
Рассмотрим проекцию этой картины на плоскость проекций 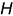. На горизонтальной проекции видно, что натуральную величину 
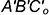треугольника 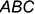определяет натуральная величина радиуса вращения 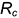точки .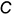
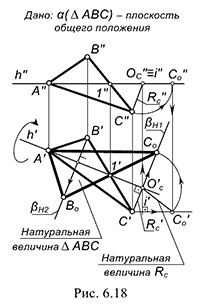
На рис. 6.18 показано построение на чертеже натуральной величины плоскости способом вращения вокруг горизонтальной прямой уровня 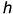. В этом случае выполняется вращение горизонтальной проекции 
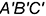треугольника, то есть вращение выполняется относительно плоскости проекций, которой параллельна ось вращения. Для решения задачи выполнен следующий графический алгоритм:
1-е действие. В заданной плоскости 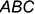провести проекции горизонтали 
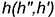, которая является осью вращения.
2-е действие. Провести следы плоскосте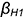й 
и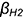 
перпендикулярно 
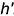, в которых будут вращаться вершины 
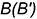и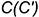 
вокруг оси вращения 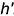; точка 
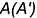будет неподвижна, так как лежит на оси вращения.
3-е действие. Определить проекции отрезка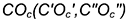 
, то есть радиуса 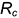вращения точки 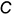вокруг горизонтали 
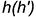и построить любым рассмотренным графическим способом натуральную величину радиуса вращения 
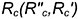; в примере натуральная величина 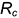построена способом вращения отрезка общего положения 
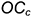вокруг фронтально-проецирую-щей оси, вырожденная проекция которой совпадает с проекцией точки 
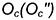(по аналогии с построениями на рис. 6.14).
4-е действие. Построенную натуральную величину радиуса вращения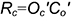 
повернуть и расположить на следе плоскости 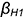, в которой вращается точка 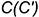треугольника, построив вершину 
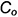в повернутом положении.
5-е действие. Достроить повернутую проекцию треугольника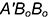 
, определив повернутую проекцию 
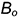вершины 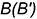на пересечении следа плоскости вращения 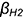с прямой, проходящей через точк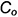и и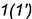 
, то есть натуральную величину радиуса вращения для точки 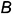определять нет необходимости — ее повернутое положение 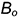определяется графическим построением.
В результате преобразования проекция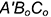 
треугольника заняла положение, параллельное горизонтальной плоскости проекций 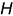и, следовательно, определяет его натуральную величину.
!!! Построение на чертеже натуральной величины плоскости 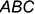вращением вокруг фронтальной прямой уровня 
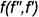выполняется аналогичными графическими действиями, только вращать следует фронтальную проекцию 
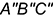треугольника, так как ось вращения 
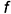параллельна фронтальной плоскости проекций. Треугольник после вращения занимает положение фронтальной плоскости уровня, которая определяет его натуральную величину (рис. 6.19).
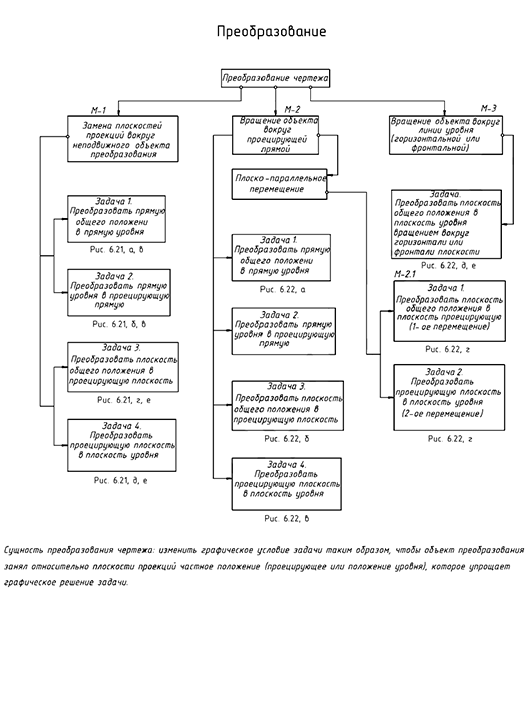
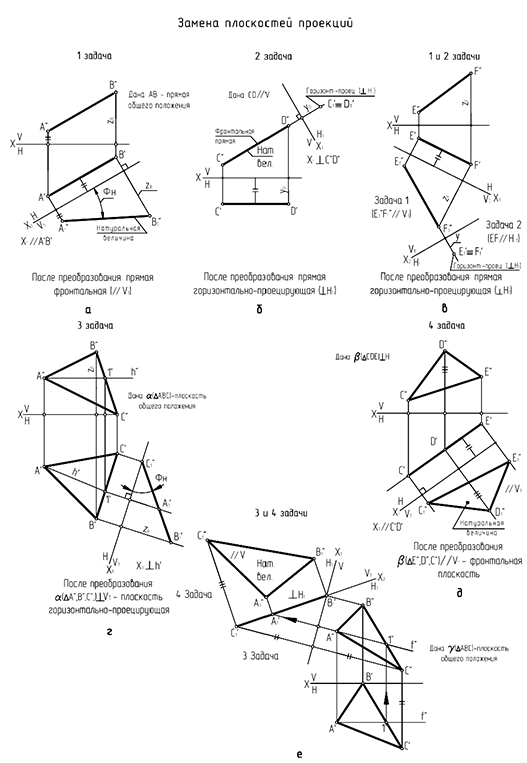
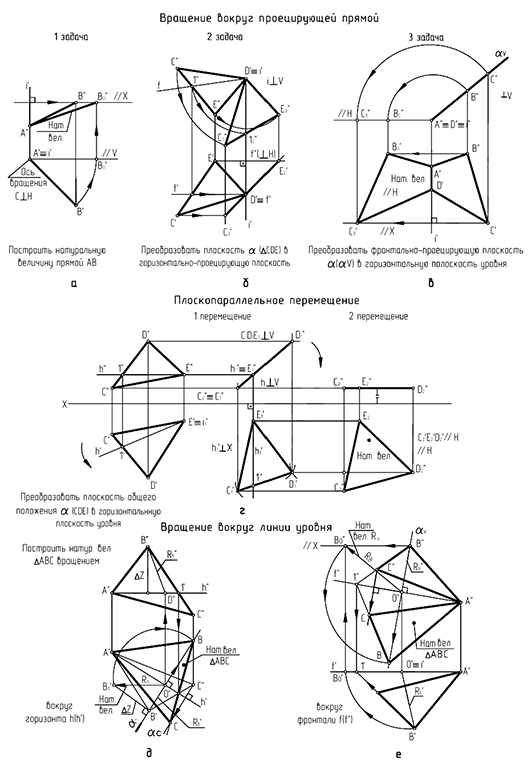
Структуризация материала шестой лекции в рассмотренном объеме схематически представлена на рис. 6.20 (лист 1). На последующих листах 2 и 3 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 6.21 и 6.22).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Способ замены (перемены) плоскостей проекций |
| Плоскопараллельное перемещение |
| Построение проекций прямой правильной призмы |
| Поверхности |
