Задача №158.
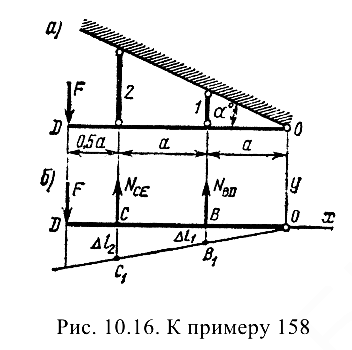
Жесткий брус 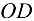 (рис. 10.16, а), шарнирно закрепленный в точке
(рис. 10.16, а), шарнирно закрепленный в точке 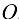 , удерживается в равновесии с помощью стержней 1 и 2. В точке
, удерживается в равновесии с помощью стержней 1 и 2. В точке 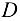 брус нагружен силой
брус нагружен силой 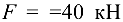 . Определить напряжения в поперечных сечениях обоих стержней, если
. Определить напряжения в поперечных сечениях обоих стержней, если 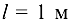 , площади поперечных сечений соответственно:
, площади поперечных сечений соответственно: 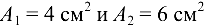 .
.
Решение:
Разрезаем стержни и заменяем их действие па брус силами 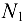 и
и 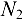 (рис. 10.16,6). В данном случае реакции шарнира
(рис. 10.16,6). В данном случае реакции шарнира 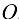 нас не интересуют, а в уравнение моментов относительно точки
нас не интересуют, а в уравнение моментов относительно точки 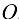 (уравнение равновесия статики)
(уравнение равновесия статики)
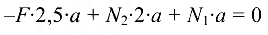
входят обе неизвестные силы. Следовательно, задача один раз статически неопределима (уравнения проекций на оси 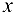 и
и 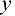 ничего не дают, так как в них войдут еще две неизвестные составляющие реакции шарнира
ничего не дают, так как в них войдут еще две неизвестные составляющие реакции шарнира 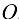 ).
).
Для того чтобы составить дополнительное уравнение перемещений, допустим, что после нагружения бруса узел 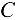 опустился на
опустился на 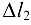 , а узел
, а узел 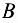 — на
— на 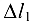 . Из подобия треугольников
. Из подобия треугольников 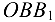 и
и 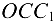 получим уравнение перемещений
получим уравнение перемещений
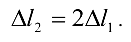
Так как
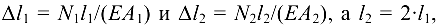
что следует из рассмотрения тех же треугольников 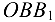 и
и 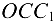 , то уравнение примет вид
, то уравнение примет вид
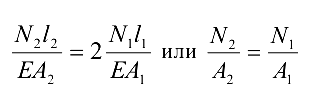
Подставив в это уравнение значения
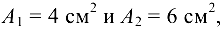
находим, что
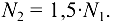
Решив совместно уравнения, получим
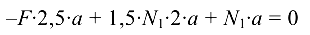
откуда
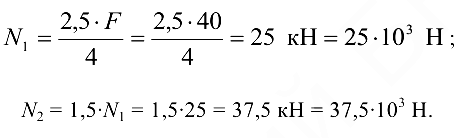
Теперь легко найти напряжения в поперечных сечениях стержней, помня, что
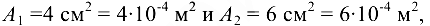
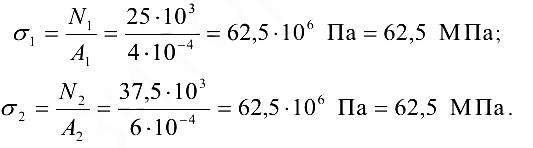
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

