Задача №100.
Для горизонтального вала, несущего два зубчатых колеса с центрами 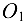 и
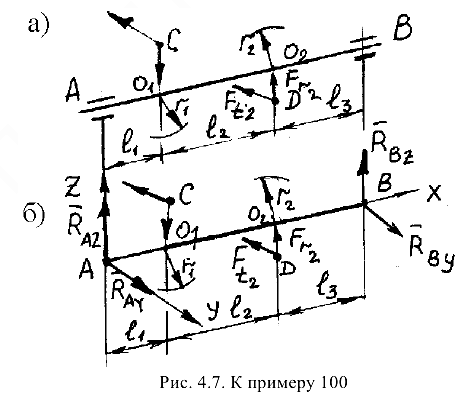
и 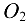 и нагруженного, как показано на рис. 4.7, а, определить реакции опор
и нагруженного, как показано на рис. 4.7, а, определить реакции опор 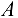 и
и 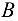 вала, если в точках
вала, если в точках 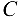 и
и 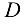 соответственно приложены силы:
соответственно приложены силы:
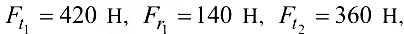
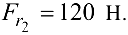
Радиусы зубчатых колес соответственно 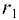 = 120 мм и
= 120 мм и 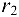 = 80 мм. Вал по длине имеет размеры
= 80 мм. Вал по длине имеет размеры
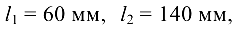
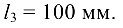
Решение:
Освобождая вал от связей (подшипников) в точках 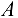 и
и 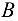 , заменяем связи их реакциями. Выбираем пространственную систему координат с началом в точке
, заменяем связи их реакциями. Выбираем пространственную систему координат с началом в точке 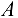 так, чтобы ось
так, чтобы ось 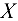 располагалась по оси вала, ось
располагалась по оси вала, ось 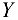 — параллельно силам
— параллельно силам 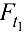 и
и 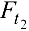 и ось
и ось 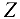 — параллельно силам
— параллельно силам 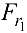 и
и 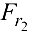 . Принимаем во внимание, что сил, действующих параллельно оси вала (оси
. Принимаем во внимание, что сил, действующих параллельно оси вала (оси 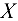 ), па схеме не имеется, в точках
), па схеме не имеется, в точках 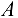 и
и 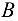 будут приложены реакции связей, располагающиеся параллельно внешним силам, приложенным к валу в точках
будут приложены реакции связей, располагающиеся параллельно внешним силам, приложенным к валу в точках 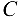 и
и 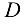 , а именно: в точке
, а именно: в точке 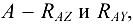 , а в точке
, а в точке 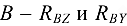 . В итоге па вал будет действовать пространственная система восьми произвольно расположенных сил:
. В итоге па вал будет действовать пространственная система восьми произвольно расположенных сил: 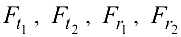 — внешние силы и
— внешние силы и 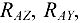
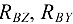 — реакции связей (рис. 4.7, б).
— реакции связей (рис. 4.7, б).
Из условия равновесия данной системы сил определим неизвестные реакции связей в опорах 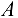 и
и 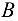 вала, составив шесть уравнений равновесия:
вала, составив шесть уравнений равновесия:
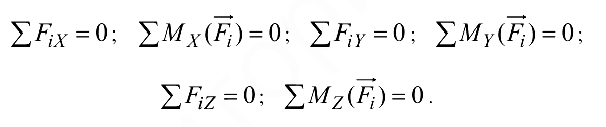
Перед составлением уравнений равновесия заметим, что, например, силы
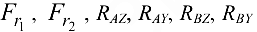
имеют моменты относительно оси 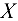 , равные нулю, потому что эти силы пересекают ось
, равные нулю, потому что эти силы пересекают ось 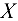 непосредственно или своим продолжением (силы
непосредственно или своим продолжением (силы 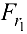 и
и 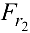 ). Силы
). Силы 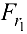 и
и 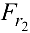 , а также
, а также  и
и 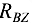 не дают моментов относительно оси
не дают моментов относительно оси 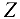 потому, что они параллельны этой оси, а сила
потому, что они параллельны этой оси, а сила  расположена на самой оси
расположена на самой оси 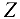 .
.
Аналогично этому моменты сил
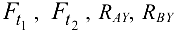
относительно оси 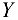 также обращаются в нуль. Уравнения равновесия системы сил принимают вид
также обращаются в нуль. Уравнения равновесия системы сил принимают вид
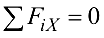
силы системы проекций на ось 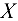 не дают;
не дают;
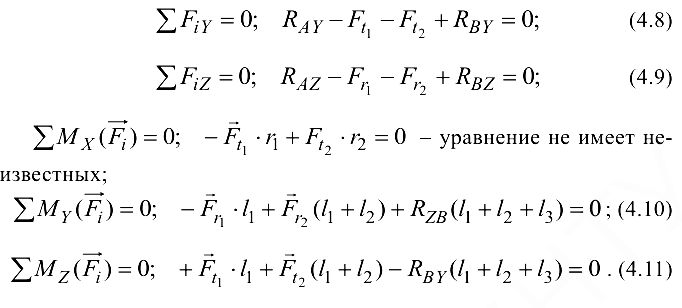
Для определения неизвестных реакций опор вала используем четыре уравнения равновесия:

Из уравнения (4.10)находим
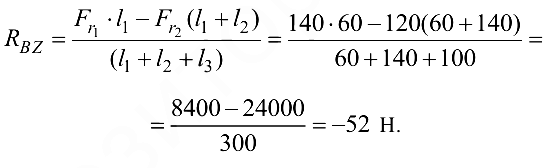
Из уравнения (4.9)
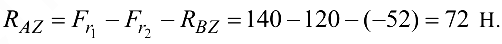
Из уравнения (4.11) находим
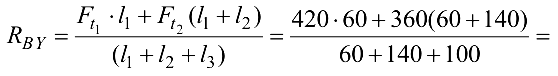
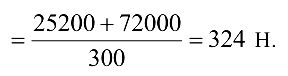
Из уравнения(4.8)
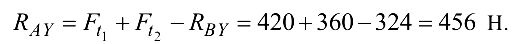
Полная реакция опоры 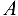
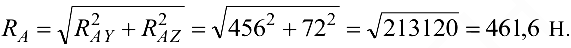
Полная реакция опоры 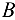
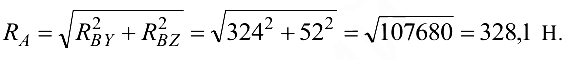
Ответ:
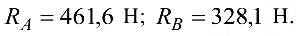
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

