Задача №79.
Для балки, изображенной па рис. 3.43, найти реакции опор, если
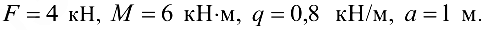
Решение:
Освободим балку от связей, мысленно отбросив опоры и приложив вместо них неизвестные реакции.
Реакция шарнирно-неподвижной опоры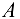 
неизвестна как по модулю, так и по направлению, поэтому изобразим ее в виде двух составляющих 
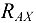и 
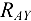, направленных вдоль выбранных осей координат 
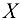и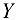 
. В шарнирно-подвижной опоре возникает одна реакция, направленная перпендикулярно плоскости, по которой она может перемещаться.
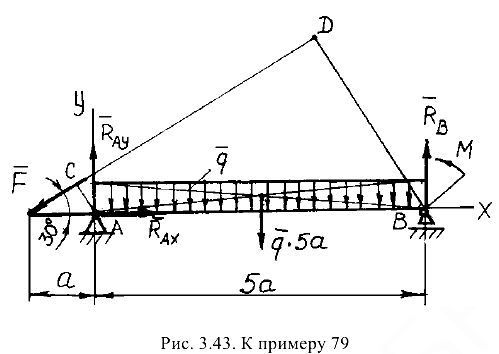
В данном случае направим реакцию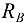 
вертикально вверх. Реакции изображены на том же рисунке, где и опоры. Система сил, действующих на балку, представляет собой плоскую систему произвольно расположенных сил, поэтому для нее можно составить три независимых уравнения равновесия. Запишем одно уравнение проекций на ось 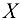и два уравнения моментов. В качестве центра моментов целесообразно принять точк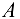и и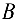 
балки. В этом случае уравнения упрощаются.
Уравнение проекций на ось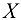 
имеет такой вид:
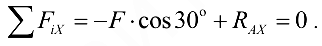
Равномерно распределенная нагрузка перпендикулярна оси 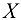, поэтому ее проекция па ось 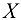равна нулю.
Уравнение моментов относительно точки 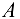имеет следующий вид:
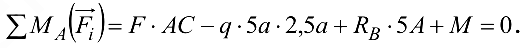
Равнодействующая равномерно распределенной нагрузки равна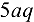 
и приложена в середине своего участка, т. е. на расстоянии 
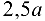от опоры .
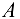Момент сосредоточенной силы и реакции 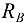, а также сосредоточенный момент вращают балку вокруг точки 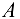против часовой стрелки, поэтому вошли в уравнение моментов со знаком «плюс», равнодействующая равномерно распределенной нагрузки вращает балку вокруг точки 
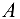по часовой стрелке, следовательно, ее момент имеет знак «минус».
Составим уравнение моментов относительно точки :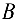
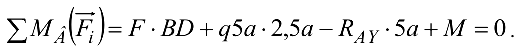
Моменты силы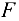 
, равнодействующей распределенной нагрузки и сосредоточенный момент 
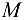направлены против часовой стрелки и войдут в уравнение моментов со знаком «плюс», а момент составляющей 
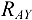, направленный по часовой стрелке, войдет со знаком «минус».
Из уравнения (3.10)
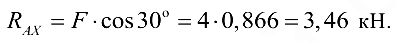
Из уравнения (3.11)
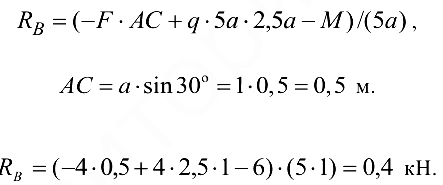
Из уравнения (3.17)
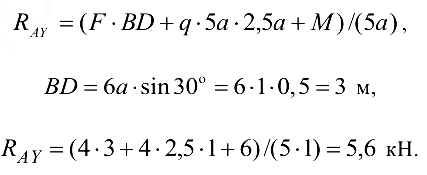
В качестве проверки используем уравнение проекций на ось :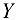
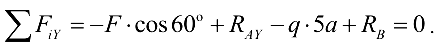
Подставив числовые значения, получим
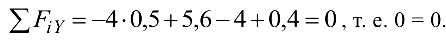
Задача решена верно.
Полная реакция опоры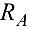 
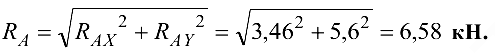
Ответ:
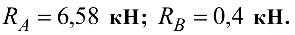
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
